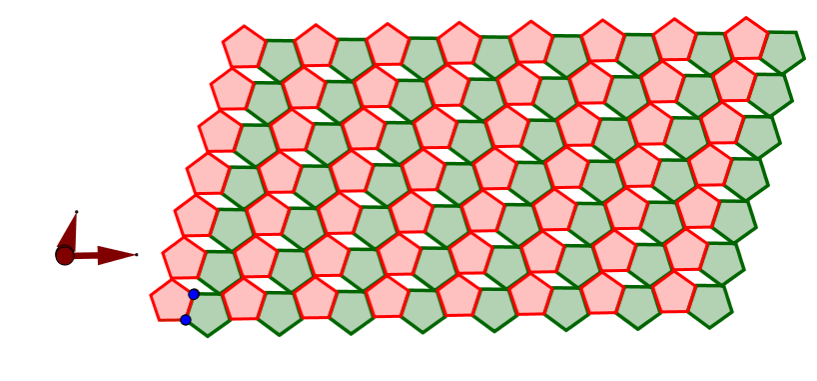
Exploring Regular Edge-Edge Tessellations of the Cartesian Plane and the Mathematics behind it
Mathematics and Art Activity - Basic Plane Tessellations with GeoGebra
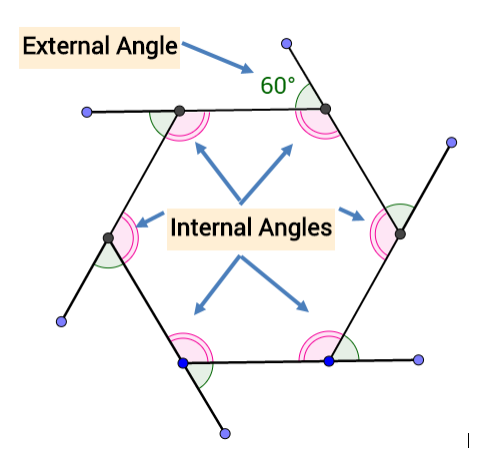
Internal and External Angles of a Regular Polygon
Symmetry
Defining a Tessellation and a Regular Tessellation of a plane
Naming convention for Regular Plane Tessellations
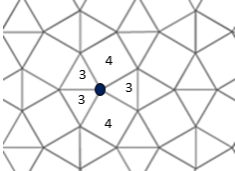
Consider the example of an edge-edge plane tessellation in Figure 1. Although all the polygons are regular, there are more than one type of polygon which that are used to tessellate. This makes this a non-regular tessellation (or tiling) of the plane.
A vertex is a common point where sides (edges) of polygons meet. The configuration of a vertex is the sequence of polygon orders that exist around it. Normally these orders are given in a sequence starting with the lowest order. The vertex configuration of each vertex in the tiling shown in Figure 1. is 3.3.4.3.4 as each vertex is surrounded by two equilateral triangles, a square, another equilateral triangle and finally a square.
Clearly the vertex configuration of each vertex of a regular tessellations of the plane will be identical.
Figure 1.
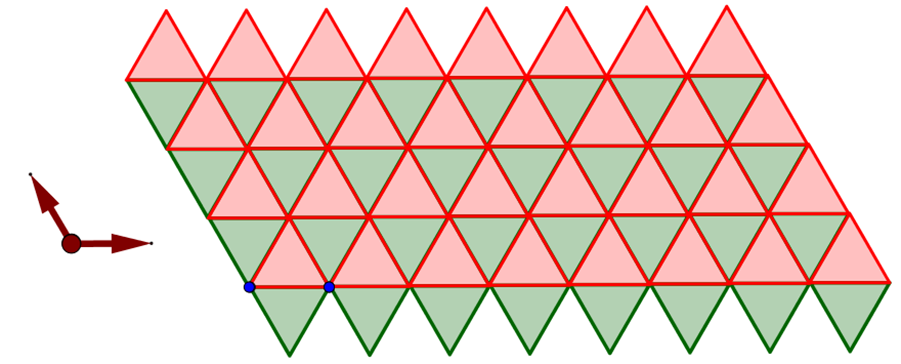
Equilateral Triangle 3.3.3.3.3.3 Tiling
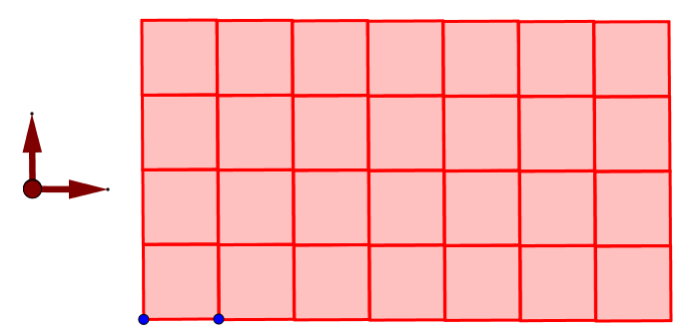
Square 4.4.4.4 Tiling
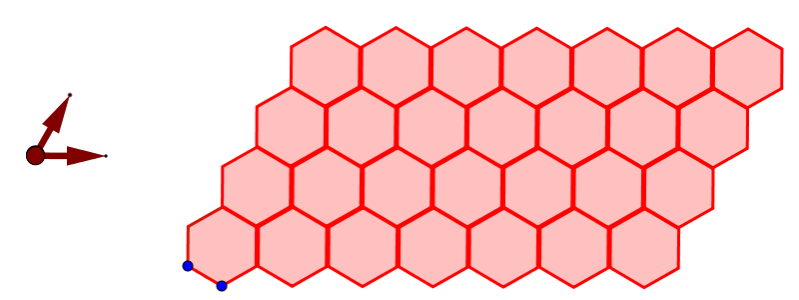
Hexagon 6.6.6 Tiling
Pentagons does not tessellate the plane - open uncovered spaces will always exist.