UM POUCO DE HISTÓRIA
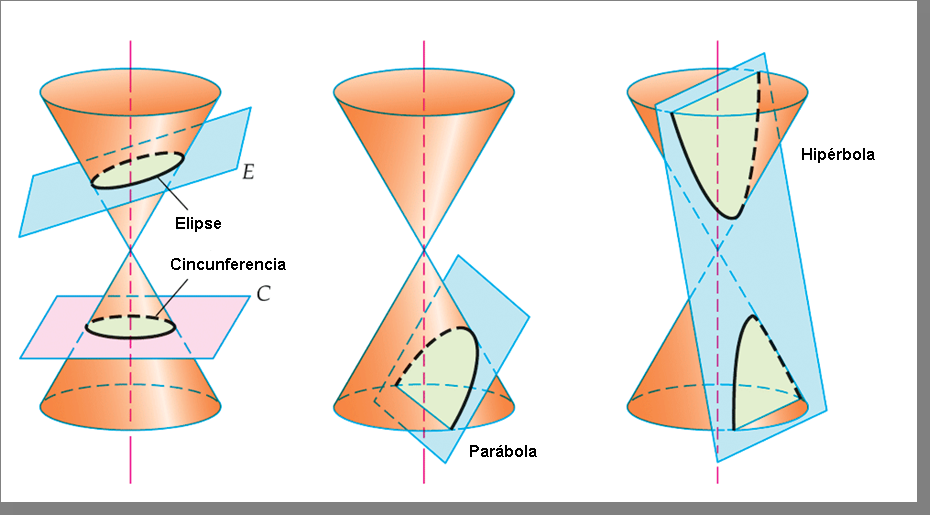
Tratados sobre as seções cônicas são conhecidos antes da época de Euclides (± 325-265 a.C.). E, associado à história dessas curvas, temos Apolônio que nasceu na cidade de Perga, região da Panfília (atualmente Turquia) por volta de 262 a.C. e viveu, aproximadamente, até 190 a.C. Apolônio foi contemporâneo e rival de Arquimedes que viveu, aproximadamente, entre 287 a.C. e 212 a.C. e, juntamente com Euclides, formam a tríade considerada como sendo a dos maiores matemáticos gregos da antiguidade. Apolônio estudou com os discípulos de Euclides em Alexandria e foi astrônomo notável, talvez ele, e não Euclides, mereceu dos antigos o adjetivo de "o grande Geômetra ". A maior parte das obras de Apolônio desapareceu. O que sabemos dessas obras perdidas devemos a Pappus de Alexandria (séc IV a.C.). Sua obra prima é Seções Cônicas composta por 8 volumes (aproximadamente 400 proposições!). Da obra original sobreviveram 7 volumes, sendo 4 escritos em grego e 3 traduzidos para o árabe por Thabit Ibn Qurra (826 a 901) no séc. IX.. Os três primeiros volumes são baseados em trabalhos de Euclides e o oitavo volume foi, infelizmente, perdido. Em 1.710, Edmund Halley traduziu os sete volumes sobreviventes de Secções Cônicas para o latim e todas as demais traduções para as línguas modernas foram feitas a partir da tradução de Halley. Os precursores de Apolônio no estudo das cônicas foram Manaecmo, Aristeu e o próprio Euclides. Nesse período, elas eram obtidas seccionando um cone circular reto de uma folha com um plano perpendicular a uma geratriz do cone, obtendo três tipos distintos de curvas, conforme a seção meridiana do cone fosse um ângulo agudo, um ângulo reto ou um ângulo obtuso. Apolônio foi o matemático que mais estudou e desenvolveu as seções cônicas na antiguidade. Suas contribuições foram: ter conseguido gerar todas as cônicas de um único cone de duas folhas, simplesmente variando a inclinação do plano de interseção; ter introduzido os nomes elipse e hipérbole e ter estudado as retas tangentes e normais a uma cônica. Fonte: http://www.sato.prof.ufu.br/Conicas/node2.html acessado em: 20/09/17