Kapitel
Funciones: curvatura y extremos relativos
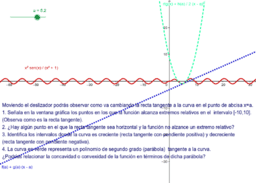
Moviendo el deslizador podrás observar como va cambiando la recta tangente a la curva en el punto de abcisa x=a. Se trata de responder a las siguientes cuestiones:
1. Señala en la ventana gráfica los puntos en los que la función alcanza extremos relativos en el intervalo [-10,10].
(Observa como es la recta tangente).
2. ¿Hay algún punto en el que la recta tangente sea horizontal y la función no alzance un extremo relativo?
3. Identifica los intervalos donde la curva es creciente (recta tangente con pendiente positiva) y decreciente
(recta tangente con pendiente negativa).
4. La curva en verde representa un polinomio de segundo grado (parábola) tangente a la curva.
¿Podrías relacionar la concavidad o convexidad de la función en términos de dicha parábola?