Teorema del seno y del coseno
Introducción
El teorema del seno y el teorema del coseno son dos resultados que establecen las relaciones entre los ángulos interiores de cualquier triángulo con el seno y coseno de los lados opuestos a los ángulos. Su aplicación permite conocer los ángulos o los lados del triángulo sin conocerlos todos. A continuación, enunciamos ambos teoremas y daremos un ejemplo de aplicación.
1. Teorema del seno
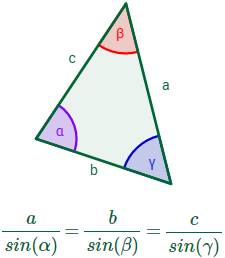
Sea un triángulo cualquiera con lados , y y con ángulos interiores opuestos , y , respectivamente, entonces
Además, si el triángulo está inscrito en una circunferencia de diámetro D,
Además, si el triángulo está inscrito en una circunferencia de diámetro D,
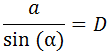
Enlace: Problemas de aplicación del Teorema del seno
Enlace: Problemas de aplicación del Teorema del seno

Además, si el triángulo está inscrito en una circunferencia de diámetro D,
Además, si el triángulo está inscrito en una circunferencia de diámetro D,
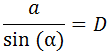
Enlace: Problemas de aplicación del Teorema del seno
Enlace: Problemas de aplicación del Teorema del seno
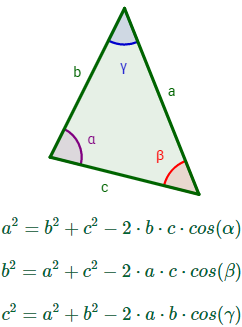
2. Teorema del coseno
Dado el triángulo del resultado anterior, el teorema del coseno establece que
Enlace: Problemas de aplicación del Teorema del seno
Enlace: Problemas de aplicación del Teorema del seno

Enlace: Problemas de aplicación del Teorema del seno
Enlace: Problemas de aplicación del Teorema del seno3. Ejemplos de aplicación
Problema 1
Calcular el ángulo del siguiente triángulo de lados , y :
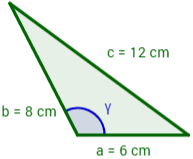 Solución:
Aplicamos la siguiente fórmula del teorema del coseno:
Solución:
Aplicamos la siguiente fórmula del teorema del coseno:
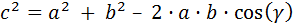
Sólo tenemos que sustituir los datos y aislar el ángulo :
Sólo tenemos que sustituir los datos y aislar el ángulo :
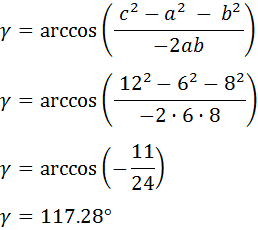
Problema 2
Calcular el radio y el diámetro de la circunferencia en la que está inscrita el siguiente triángulo del que sólo se conoce el ángulo :
Problema 2
Calcular el radio y el diámetro de la circunferencia en la que está inscrita el siguiente triángulo del que sólo se conoce el ángulo :
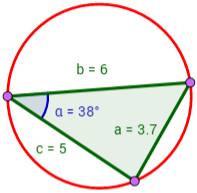 Solución:
El teorema del seno proporciona el diámetro D:
Solución:
El teorema del seno proporciona el diámetro D:
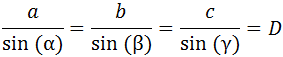
Conociendo ángulo y su lado opuesto, , podemos calcular el diámetro:
Conociendo ángulo y su lado opuesto, , podemos calcular el diámetro:
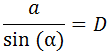
Sustituimos los datos:
Sustituimos los datos:
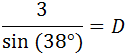
Luego el diámetro mide
Luego el diámetro mide
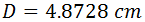
 Solución:
Aplicamos la siguiente fórmula del teorema del coseno:
Solución:
Aplicamos la siguiente fórmula del teorema del coseno:
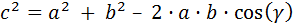
Sólo tenemos que sustituir los datos y aislar el ángulo :
Sólo tenemos que sustituir los datos y aislar el ángulo :
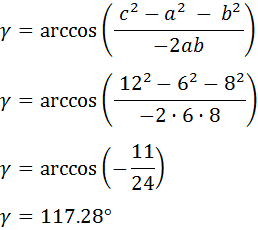
Problema 2
Calcular el radio y el diámetro de la circunferencia en la que está inscrita el siguiente triángulo del que sólo se conoce el ángulo :
Problema 2
Calcular el radio y el diámetro de la circunferencia en la que está inscrita el siguiente triángulo del que sólo se conoce el ángulo :
 Solución:
El teorema del seno proporciona el diámetro D:
Solución:
El teorema del seno proporciona el diámetro D:
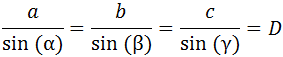
Conociendo ángulo y su lado opuesto, , podemos calcular el diámetro:
Conociendo ángulo y su lado opuesto, , podemos calcular el diámetro:
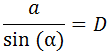
Sustituimos los datos:
Sustituimos los datos:
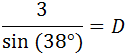
Luego el diámetro mide
Luego el diámetro mide