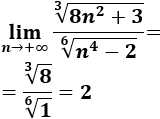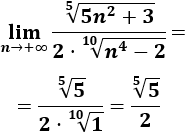Límites de Sucesiones
En este texto vamos a calcular algunos límites de sucesiones.
Los razonamientos que seguimos para el cálculo de límites de sucesiones son los mismos que los que seguimos para el de límites de funciones (una sucesión es una función definida sobre los naturales). Esto significa que en los límites de las sucesiones pueden aparecer indeterminaciones que ya sabemos cómo resolver: cálculo de límites e indeterminaciones.
Recordatorio
Una sucesión a(n) es convergente a L≠∞ (L es finito) si
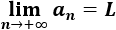 En este caso dice que la sucesión a(n) converge a su límite L y lo expresamos por a(n)→L. En caso contrario, la sucesión diverge.
Aclaraciones:
En este caso dice que la sucesión a(n) converge a su límite L y lo expresamos por a(n)→L. En caso contrario, la sucesión diverge.
Aclaraciones:
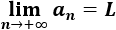 En este caso dice que la sucesión a(n) converge a su límite L y lo expresamos por a(n)→L. En caso contrario, la sucesión diverge.
Aclaraciones:
En este caso dice que la sucesión a(n) converge a su límite L y lo expresamos por a(n)→L. En caso contrario, la sucesión diverge.
Aclaraciones:
- Si el límite de a(n) es +∞ ó −∞, la sucesión diverge.
- Si el límite de a(n) no existe, la sucesión diverge.
- La sucesión a(n) sólo converge cuando su límite es finito.
1. Límite de a(n) = 5/n
El límite de la sucesión es 0 porque el grado del denominador es mayor que el del numerador:
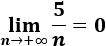 2. Límite de a(n) = 3 - 2/n
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
2. Límite de a(n) = 3 - 2/n
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
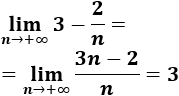 3. Límite de a(n) = n^2/(n + 1)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
3. Límite de a(n) = n^2/(n + 1)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
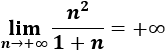 4. Límite de a(n) = (n^2 - 2)/(2n^2 - 1)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
4. Límite de a(n) = (n^2 - 2)/(2n^2 - 1)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
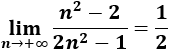
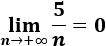 2. Límite de a(n) = 3 - 2/n
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
2. Límite de a(n) = 3 - 2/n
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
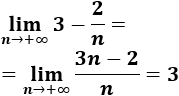 3. Límite de a(n) = n^2/(n + 1)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
3. Límite de a(n) = n^2/(n + 1)
El límite de la sucesión es infinito porque el grado del numerador es mayor que el del denominador:
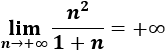 4. Límite de a(n) = (n^2 - 2)/(2n^2 - 1)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
4. Límite de a(n) = (n^2 - 2)/(2n^2 - 1)
El límite de la sucesión es el cociente de los coeficientes directores del numerador y del denominador (porque tienen el mismo grado):
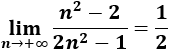
Finalmente, calculamos el límite de la sucesión
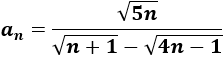
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):

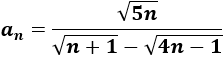
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):
El grado del numerador y el del denominador son el mismo, pero tal y como está escrita la sucesión, no sabemos cuál es el coeficiente director del denominador. Tenemos que operar un poco (multiplicar y dividir por el conjugado del denominador):

Más ejercicios: Cálculo de límites de sucesiones o progresiones
Otros temas de progresiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente
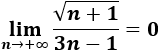 El grado del numerador es 1/2 y el del denominador es 1. Por tanto, tiende a 0.
Límite 2
El grado del numerador es 1/2 y el del denominador es 1. Por tanto, tiende a 0.
Límite 2