DEFINICE FUNKCE
FUNKCE
Funkce je množina uspořádaných dvojic reálných čísel (dále již jen čísla). Tato množina musí splňovat funkční kritérium, které ji odlišuje od jiných množin uspořádaných dvojic: "Žádné číslo na první pozici (toto číslo nazýváme vzorem) nesmí být v uspořádané dvojici se dvěma různými čísly na druhé pozici (těmto číslům říkáme obrazy). " Vzory a obrazy označujeme jako proměnné, vzory písmenem x (nezávislé) a obrazy písmenem y (závislé).
Množinový zápis funkce obvykle nepoužíváme ve tvaru f = {[1; 2], [3; 5], [10; 7]}. Místo něj uspořádané dvojice píšeme do tabulky:
f:
Řádek tabulky se vzory vytváří číselnou množinu . Tato množina se nazývá definiční obor funkce. Označuje se písmenem D, za které do závorky píšeme název funkce. Podobně druhý řádek tabulky vytváří množinu , která se nazývá obor hodnot a označuje se písmenem H a jménem funkce.
Jak si funkce představit
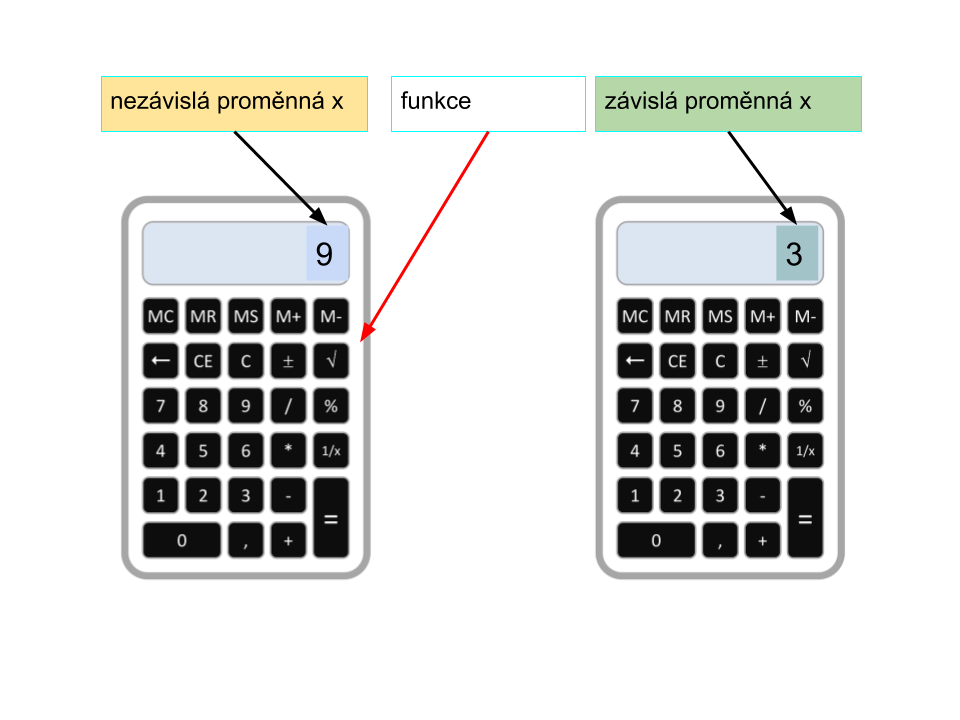
Funkci si můžete představit jako stroj na výrobu čísel (např. kalkulačku). Do stroje jedno číslo zadáváme (číslo z definičního oboru, jinak vám stroj žádnou odpověď neposkytne) a stroj vám z něj vyrobí číslo jiné (na kalkulačce po zadání prvního čísla stisknete funkční klávesu, třeba s druhou odmocninou, a kalkulačka vám vyrobí a na displeji zobrazí druhé číslo). Z toho je patrné, proč se první proměnná nazývá nezávislá proměnná. Toto číslo zadávám do kalkulačky podle potřeby já. Druhé číslo, které kalkulačka poskytne jako výsledek, závisí na mé volbě prvního čísla, a proto se proměnná y nazývá závislá.
| x | 1 | 3 | 10 |
| y | 2 | 5 | 7 |
FUNKCE JAKO STROJ