La Función Afín
La expresión general es 
. Con 
Su dominio es R y es continua en todo R.
(Su representación gráfica es una recta).
“m” se llama pendiente y, cuanto mayor sea ésta, mayor es la inclinación de la recta que la representa.
. Con
Su dominio es R y es continua en todo R.
(Su representación gráfica es una recta).
“m” se llama pendiente y, cuanto mayor sea ésta, mayor es la inclinación de la recta que la representa.
- Si m > 0, la recta es creciente.
- Si m < 0, la recta es decreciente.
La función afín es de la forma:
Distintas formas de encontrar la ecuación de una recta:
, después elegimos uno de los puntos y lo sustituimos en y=mx+n.
- Conocidos dos puntos A(x0,y0) y B(x1,y1).
, después elegimos uno de los puntos y lo sustituimos en y=mx+n.- Pasa por un punto A(x0,y0) y tiene pendiente m.
Tipos de funciones lineales
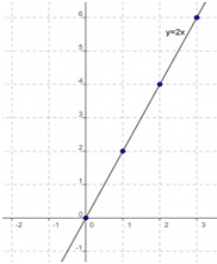
FUNCIÓN DE PROPORCIONALIDAD y=mx
Siempre pasa por el punto (0,0).
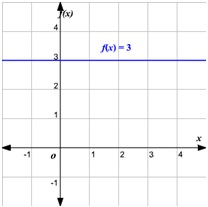
FUNCIÓN CONSTANTE y=n
Es paralela al eje de abscisas.
Ejemplo 1:
Encontrar la ecuación de la función afín que pasa por los puntos de coordenadas (-1,3) y (4,7).
(Solución: 
)
Ejemplo 2:
La compañía telefónica nos cobra mensualmente, 4 € por alquiler de la línea y 40 céntimos de euro por cada minuto hablado. Escribe la ecuación de la función que nos da el gasto en relación de los minutos hablados.
a) ¿Cuánto habrá que pagar si hemos hablado 2 horas?
b) ¿Cuántos minutos hemos hablado si hemos pagado 35 €?
(Solución: La función es: y=0,4x+4 , donde x son los minutos hablados e y el gasto, en €. a) 52 € b) 1h 17min 30s)
)
Ejemplo 2:
La compañía telefónica nos cobra mensualmente, 4 € por alquiler de la línea y 40 céntimos de euro por cada minuto hablado. Escribe la ecuación de la función que nos da el gasto en relación de los minutos hablados.
a) ¿Cuánto habrá que pagar si hemos hablado 2 horas?
b) ¿Cuántos minutos hemos hablado si hemos pagado 35 €?
(Solución: La función es: y=0,4x+4 , donde x son los minutos hablados e y el gasto, en €. a) 52 € b) 1h 17min 30s)TRASLACIÓN DE UNA FUNCIÓN
Traslaciones Verticales: y = f(x)+k
- Si k > 0 se desplaza la función k unidades hacia arriba.
- Si k < 0 se desplaza la función k unidades hacia abajo
- Si h > 0 se desplaza la función h unidades hacia la izquierda.
- Si h < 0 se desplaza la función h unidades hacia la derecha.
