moltiplicazione e roto-omotetie
Moltiplicazione A∙B con A e B entrambi punti del piano cartesiano.
A∙B è il punto realizzato nel sistema di riferimento ( 0 , B , B⊥ )
con le coordinate che A ha nel sistema di riferimento ( 0 , 1 , i ),
ossia con A_x e A_y .
Vedi ▶ http://tinyurl.com/moltiplicazione
In questa figura è il punto A a variare; e il punto B, che è fisso, stabilisce la rotazione e l'ingrandimento/rimpicciolimento.
Costruire BA o AB dà luogo allo stesso punto
(proprietà commutativa della moltiplicazione tra punti):
A = p*1 + q*i = (p,q) ---> A⊥= (-q,p) = -q+pi
B=r*1+s*i=(r,s) ---> B⊥=(-s,r)=-s+ri
AB = p*B + q*B⊥ = p(r+si) + q(-s+ri)
BA = r*A+s*A⊥ = r(p+qi) + s(-q+pi) -
--> AB=BA
roto-omotetie in C
- roto-omotetia di rapporto w: è l' omotetia in C già considerata nella fase precedente; poniamo la definizione: Rw : z
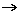 z•w, ossia Rw(z) := z•w.
Rw è anche detta roto-omotetia di fattore w
z•w, ossia Rw(z) := z•w.
Rw è anche detta roto-omotetia di fattore w
- la roto-omotetia Rw : C
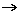 C estende da R a C la parametrizzazione Lw : R
C estende da R a C la parametrizzazione Lw : R 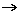 R•w
R•w
- Quando w=x è reale si ha: Rx(z)=z•x=x•z=Hx(z). Le roto-omotetie generalizzano le omotetie (in quanto diventano omotetie se il fattore è reale)
- proprietà delle roto-omotetie:
- composizione di roto-omotetie: Rv
 Rw = Rvw
Rw = Rvw - azione sulle unità: Rw(1)=w e Rw(i)=ort(w)
- commutatività: Rw
 Rv = Rv
Rv = Rv Rw
Rw - associatività: come per traslazioni e omotetie
- azione sul coniugato del fattore: Rw(w) ≥ 0 (prova a dimostrare queste proprietà)
- Approfondimento: la formula di Eulero e le funzioni seno e coseno