Геометрическое определение

Обычно тригонометрические функции определяются геометрически. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса  с центром в начале координат . Всякий угол можно рассматривать как поворот от положительного направления оси абсцисс до некоторого луча , при этом направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным. Абсциссу точки  обозначим , ординату обозначим (см. рис. 1).

• Синусом называется отношение 
• Косинусом называется отношение 
• Тангенс определяется как 
• Котангенс определяется как 
• Секанс определяется как 
• Косеканс определяется как 

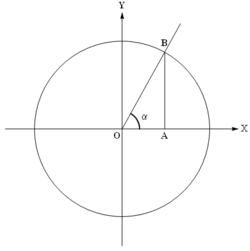
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности  в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате , а косинус — абсциссе . На рисунке 2 показаны величины тригонометрических функций для единичной окружности.

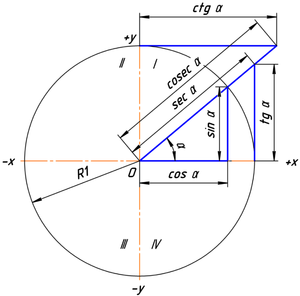
Если α — вещественное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.