Démonstration
Soient trois points , et non alignés et deux à deux distincts.
Soit et tels que les points , , soient alignés dans le même ordre que les points , , .
On pose tel que .
Nous avons d'après le Théorème de Thalès :
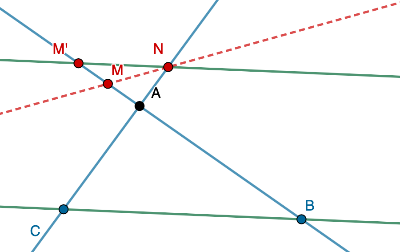
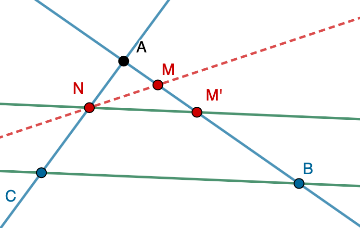
Si :
Nous avons alors
Et donc , les points et sont alors confondus
Et donc par hypothèse