Equação reduzida da reta: y=mx+n
Desde suas origens, a geometria analítica é um campo privilegiado para as conexões entre a álgebra e a geometria. É sabido que a escolha de um sistema de coordenadas permite que se
estabeleça uma estreita relação entre, de um lado, figuras geométricas e, de outro, equações (ou inequações) envolvendo as coordenadas dos pontos.
Na geometria analítica,tanto se resolvem problemas geométricos recorrendo a métodos algébricos, quanto se atribui significado geométrico a fatos algébricos. Também nesse momento, o recurso aos gráficos cartesianos permite importantes conexões entre objetos matemáticos
distintos e inter-relacionados: função, equação e figura geométrica.
É indispensável que o aluno compreenda, por exemplo, que a reta que ele encontra na geometria
analítica não é um objeto matemático distinto do gráfico de uma função de 1º grau.
Uma equação reduzida da reta respeita a lei de formação dada por y = mx + n, onde x e y são os pontos pertencentes à reta.
- m é o coeficiente angular da reta
- c o coeficiente linear.
Essa forma reduzida da equação da reta expressa uma função entre x e y, isto é, as duas variáveis possuem uma relação de dependência. No caso dessa expressão, ao atribuirmos valores a x (eixo das abscissas), obtemos valores para y (eixo das ordenadas).
No caso de funções matemáticas do 1º grau, estamos relacionando o domínio (x) de uma função com sua imagem (y).
Outra característica desse modelo de representação é quanto ao valor do coeficiente
angular e linear.
O coeficiente angular (m)representa a inclinação da reta em relação ao eixo das abscissas (x) e o coeficiente linear (n) representa o valor numérico por onde a reta passa no eixo das ordenadas (y).
Considere ax + by + c = 0 como sendo a equação geral de uma reta não vertical. Isolando y na equação geral obtemos:
Fazendo
Teremos:
y =mx + n → que é a equação reduzida da reta.
m = tgα,em que α é o ângulo formado entre a reta e o eixo x.
m é chamado de coeficiente angular da reta ou declividade da reta. É o ponto onde a reta corta
o eixo x.
n é chamado de coeficiente linear da reta e é o ponto onde a reta corta o eixo y.
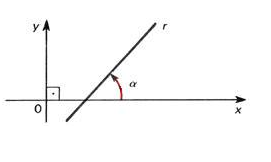
Podemos representar uma reta no plano cartesiano por meio da condição geométrica ou por uma equação matemática. Em relação à equação matemática, a reta pode ser escrita nas seguintes formas:
reduzida, segmentária, geral ou paramétrica. Vamos abordar a representação de
uma equação reduzida de reta,demonstrando três possíveis situações.
Vamos construir a equação reduzida de uma reta de acordo com os pontos P(2, 7) e Q(–1, –5) pertencentes à reta. Para determinar essa equação há duas maneiras, observe:
1º maneira
Calcular o coeficienteangular (m) através da fórmula
Determinar o coeficienteangular da reta.
m =(y2 – y1) / (x2 – x1)
m =(–5 – 7) / (–1 – 2)
m =–12 / –3
m = 4
De acordo com o ponto P(2,7), temos:
y – y1 = m * (x – x1)
y – 7= 4 * (x – 2)
y – 7= 4x – 8
y =4x – 8 + 7
y =4x – 1
2ª maneira
Resolver o sistema de equaçãoformado pelos pontos P e Q
Temosque a lei de formação de uma equação reduzida da reta é dada por y = mx + n.
Considerando que ela passapor P(2, 7) e Q(–1, –5), temos:
Nesse caso, os valores dos coeficientes angular (a) e linear(b) serão calculados por um sistema de equações. Veja:
P(2, 7)
7 = m* 2 + n
7 =2m + n
2m + n = 7
Q(–1, –5)
–5 =m * (–1) + n
–5 =–m + n
–m + n = –5
Resolvendo o sistema,
2m + n = 7
–m + n = –5
determinamos o coeficiente angular m=4 e o coeficiente linear n=1.
Portanto, a equação reduzida da reta y = mx + n que passapelos pontos P(2, 7) e Q(–1, –5), corresponde à expressão y = 4x – 1.
Observações:
Se a reta for horizontal, ela forma um ângulo nulo com o eixo x. Assim, m = tg 0o e a equação reduzida da reta será dotipo y = c
Se a reta for vertical, ela forma um ânguloreto com o eixo x e, como não existe tg 90o, não é possível escrever a equação reduzida da reta.