Võrdeline sõltuvus
1. Võrdeline sõltuvus
Mõndasid muutujatevahelisi seoseid (funktsioone) tuntakse matemaatikas omaette nimetuste all. Näiteks võrdelist sõltuvust kohtame igapäeva elus sagedasti. Mida aga tähendab ütlus, et muutujad on omavahel võrdelises sõltuvuses?
Näide 1. Oletame, et lähed sõpradega poodi ja igaüks teist ostab komme. Esimene sõber ostab 1 kg komme ja tasub 9 eurot. Teine sõber ostab 0,5 kg ja maksab 4,5 eurot. Kolmas sõber ostab aga 1,5 kg ja tasub 13,5 eurot. Ise ostad 2 kg komme ja tasud 18 eurot.
Kas saame öelda, et kõik ostjad ostsid ühe ja sama hinnaga komme? Kuidas seda kindlaks teha? On teada mitu kg igaüks ostis ja palju maksma läks. Saame leida iga ostja poolt makstud rahasumma ja ostetud koguse kaudu 1 kg kommide hinna. Jagame tasutud rahasumma ostetud kommide kogusega, mille tulemusena saamegi kommide 1 kg hinna.

Näeme, et muutujad (kogus ja hind) on seotud nii, et nende vastavate väärtuste jagatis on jääv (1 kg hind). Kahte suurust, mille vastavate väärtuste suhe (jagatis) on jääv nimetatakse võrdelisteks suurusteks. Kui kaks muutujat ja on sellises sõltuvuses, et ehk , siis seda sõltuvust nimetatakse võrdeliseks sõltuvuseks. Seos on funktsioon, sest muutuja iga võimaliku väärtuse järgi saab leida muutuja ühe kindla väärtuse. Jäävat suhet () nimetatakse nende suuruste võrdeteguriks. Sealjuures öeldakse, et muutuja on võrdeline muutujaga .
Seega antud näite puhul võrdelisteks suurusteks on kommide kogus ja maksumus, ning võrdeteguriks on 1 kg kommide hind. Kusjuures antud suuruste kommide koguse ja maksumuse vahel on võrdeline sõltuvus . Kuna vastavate väärtuste jagatis on jääv, siis järelikult kõik ostjad ostsid tõepoolest ühe ja sama hinnaga komme.
Näide 2. Rongiga Tartust-Tallinnasse sõites tuleb läbida 190 km, mis võtab aega umbes 2,5 tundi. Rong teeb kaks vahepeatust: Rakkel ja Kehra. Rakkele sõidab rong Tartust umbes 1 h ja Kehra umbes 2 h. Kuidas leida, mitme kilomeetri kaugusel asuvad Rakke ja Kehra Tartust?
Rongi liikumine on mitteühtlane st võrdsetes ajavahemikes läbib keha erinevad teepikkused. Rongi liikumist võivad mõjutada erinevad tegurid nt raudtee kuju, pinnamood ja peatuste tegemine. Kuidas siiski ligikaudselt hinnata, millal rongi vahepeatustesse oodata?
Mõõtes kogu läbitud teepikkuse ja leides läbitud teepikkuse, ning selle läbimiseks kulunud aja jagatisena saame kiiruse. Leitud kiirus ei tähenda aga seda, et rong tegelikkuses sellise kiirusega sõitis. Kiirus võis muutuda antud vahemikus, ning välistatud pole seegi variant, et rong üldse sellist kiirust antud vahemikus omas. Ometigi iseloomustab arvutatud kiirus rongi sõitu ja võimaldab ligikaudselt välja arvutada kaua võib rongil aega kuluda ühest peatusest teise jõudmiseks.
Selliselt arvutatud kiirust nimetatakse keskmiseks kiiruseks. Keskmine kiirus on läbitud teepikkuse () ja selle läbimiseks kulunud aja () suhe (jagatis) . Keskmine kiirus näitab kui pikk tee läbitakse keskmiselt mingi ajaühiku jooksul. Teepikkus () ja selle läbimiseks kulunud aeg () on võrdelises sõltuvuses () st teepikkus on võrdeline ajaga, ning võrdeteguriks on keskmine kiirus .
Igasuguste sõidugraafikute koostamisel võetatakse aluseks keskmine kiirus. Seega Tartu-Rakke ja Tartu-Kehra vahemaa leidmiseks tuleb esmalt kindlaks teha, millise kiirusega läbitakse Tartu-Tallinn vahemaa. Kasutades keskmise kiiruse arvutamise valemit saame, et rongi keskmine kiirus vahemaa läbimisel on km/h st rong läbib igas tunnis keskmiselt 76 km. Leiame nüüd Tartu-Rakke ja Tartu-Kehra vahelise kauguse. Kasutame läbitud teepikkuse ja selle läbimiseks kulunud aja seost . Tartust Rakkesse on km ja Tartust Kehrasse on km.
Seega, et teada saada kui kaugel asuvad Kehra ja Rakke Tartust, tuli välja selgitada esmalt kui pika vahemaa rong keskmiselt ühe tunni jooksul läbib (), ning seejärel kasutada läbitud teepikkuse leidmise valemit .
Näide 3. Ruudu ümbermõõdu valemist ilmneb, et ruudu übermõõt on võrdeline tema külje pikkusega . See tähendab seda, et mistahes ruudu külje pikkuse () korral ümbermõõdu ja ruudu külje suhe on jääv (võrdetegur ).
Kuna võrdetegur saab olla ainult positiivne () ja muutujate ( ja ) väärtused samuti positiivsed, siis neid muutujaid seob üks omadus: ühe muutuja väärtuse suurenemisel (või vähenemisel) mingi arv korda suureneb (või vastavalt väheneb) ka teise muutuja väärtus sama arv korda.
Näide 4. On teada, et inimese süda pumpab ühe ööpäeva jooksul umbes 7,5 liitrit verd. Väljendame valemina südame pumpamise aja tundides () ja pumbatud vere koguse liitrites (). Arvutame saadud valemi järgi, kui palju verd pumpab inimese süda 1 tunni, 7 päeva (1 nädala), 30 päeva (keskmiselt 1 kuu), 365 päeva (1 aasta) jooksul, ning koostame algandmete ja saadud tulemuste põhjal tabeli.
Saame koostada valemi . Näeme, et pumbatud vere kogus () on võrdeline pumpamise ajaga () st , kus võrdetegur on .
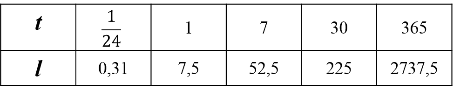
Seega kui on teada, et 1 ööpäeva ehk 24 tunni jooksul pumpab inimese süda liitrit verd, siis 1 tunni jooksul pumpab inimese süda -st liitrist ehk liitrit verd. 7 päeva jooksul pumpab süda liitrit, 30 päeva jooksul liitrit ja 365 päeva jooksul liitrit verd.
Esitame seose ka tabelina: