Sucesiones alternadas y oscilantes
Una sucesión es alternada cuando cada término tiene el signo contrario que el del término que le precede.
Una sucesión es oscilante cuando:
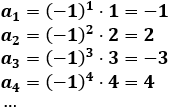 Observad que los signos se alternan: negativo, positivo, negativo, positivo...
Representación de la sucesión (n≤10):
Observad que los signos se alternan: negativo, positivo, negativo, positivo...
Representación de la sucesión (n≤10):
 La potencia (−1)^n es positiva cuando n es par y negativa cuando n es impar. Es el causante de la alternancia del signo.
La sucesión no es convergente.
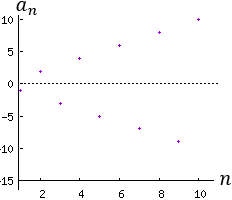
Ejemplo 2: La sucesión a(n) = (-1)^n/n es alternada y convergente:
La potencia (−1)^n es positiva cuando n es par y negativa cuando n es impar. Es el causante de la alternancia del signo.
La sucesión no es convergente.
Ejemplo 2: La sucesión a(n) = (-1)^n/n es alternada y convergente:
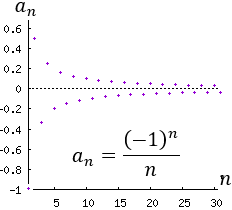 Ejemplo 3: La sucesión a(n) = -1 si n es par y a(n) = 5 si n es impar es alternada.
Calculamos los 10 primeros términos:
Ejemplo 3: La sucesión a(n) = -1 si n es par y a(n) = 5 si n es impar es alternada.
Calculamos los 10 primeros términos:
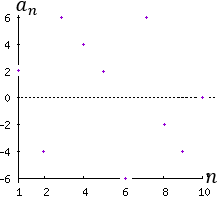
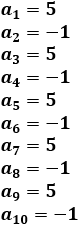 Ejemplo 4: La sucesión 2, -4, 6, 4, 2, -6, 6, -2, -4, 0, -2, 2,... es oscilante. Representación de la sucesión (n≤10):
Ejemplo 4: La sucesión 2, -4, 6, 4, 2, -6, 6, -2, -4, 0, -2, 2,... es oscilante. Representación de la sucesión (n≤10):
 Recursos de sucesiones o progresiones:
Recursos de sucesiones o progresiones:
- no es alternada y
- no es creciente ni decreciente ni constante.
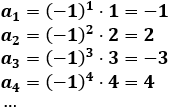 Observad que los signos se alternan: negativo, positivo, negativo, positivo...
Representación de la sucesión (n≤10):
Observad que los signos se alternan: negativo, positivo, negativo, positivo...
Representación de la sucesión (n≤10):
 La potencia (−1)^n es positiva cuando n es par y negativa cuando n es impar. Es el causante de la alternancia del signo.
La sucesión no es convergente.
Ejemplo 2: La sucesión a(n) = (-1)^n/n es alternada y convergente:
La potencia (−1)^n es positiva cuando n es par y negativa cuando n es impar. Es el causante de la alternancia del signo.
La sucesión no es convergente.
Ejemplo 2: La sucesión a(n) = (-1)^n/n es alternada y convergente:
 Ejemplo 3: La sucesión a(n) = -1 si n es par y a(n) = 5 si n es impar es alternada.
Calculamos los 10 primeros términos:
Ejemplo 3: La sucesión a(n) = -1 si n es par y a(n) = 5 si n es impar es alternada.
Calculamos los 10 primeros términos:
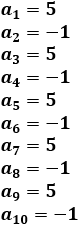 Ejemplo 4: La sucesión 2, -4, 6, 4, 2, -6, 6, -2, -4, 0, -2, 2,... es oscilante. Representación de la sucesión (n≤10):
Ejemplo 4: La sucesión 2, -4, 6, 4, 2, -6, 6, -2, -4, 0, -2, 2,... es oscilante. Representación de la sucesión (n≤10):
 Recursos de sucesiones o progresiones:
Recursos de sucesiones o progresiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente