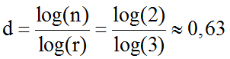Fractale dimensie
Waarom zeggen we dat een lijnstuk dimensie 1 heeft, een rechthoek dimensie 2 en een kubus dimensie 3?
Deze objecten proberen we ook op te vatten als ‘zelfgelijkvormig’.
Voorbeeld: een lijnstuk
We kunnen een lijnstuk (met dimensie 1) verdelen in bijvoorbeeld 5 zelfgelijkvormige kopieën
van zichzelf (n = 5), waarbij de reductiefactor gelijk is aan 5 (r = 5).
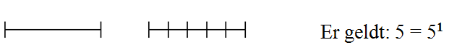
Voorbeeld: een rechthoek
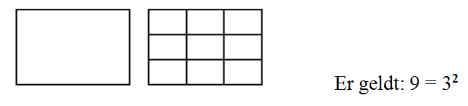
Een rechthoek (met dimensie 2) kunnen we ook bekijken als zelfgelijkvormig met bv. 9 verkleinde kopieën van zichzelf (n = 9). De reductiefactor is hierbij gelijk aan 3 (r = 3).
Voorbeeld: een kubus
Een kubus (met dimensie 3) kan verdeeld worden in bv. 27 zelfgelijkvormige kubusjes
(n = 27) met reductiefactor 3 (r = 3). Als afbeelding nemen we de gekende Rubik’s kubus.

Algemeen
We zien dus dat voor de dimensie d van een meetkundig object steeds de algemene formule geldt:
n = rd
met n = het aantal zelfgelijkvormige stukjes en r = de reductiefactor.Berekening van fractale dimensie d
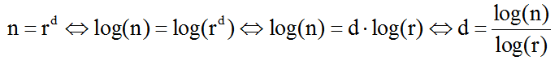
Voorbeeld: fractale dimensie Cantor-set