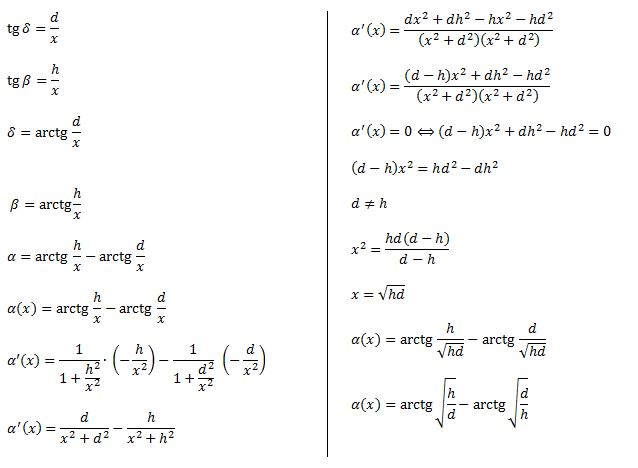Legjobb oldalpáholy megtalálása függvénnyel
Feladat, problémafelvetés, célkitűzés
Színházjegy vásárlásakor melyik földszinti oldalpáholy helyeket válasszuk, hogy a lehető legjobban lássuk a színpadot? A megoldáshoz a távolság – szög függvény vizsgálata vezet el.
Tegyük fel, hogy a színház alaprajza felülnézetből tengelyesen szimmetrikusan helyezkedik el.
Alkalmazás
1. kérdés
Ismerkedés: a csúszkák segítségével beállítható a nézőtér és színpad szélessége. A P pont jelöli az oldalpáholyon azt a helyet, melyből a színpadot figyeljük.
2. kérdés
Figyeld meg mi történik, ha P pontot mozgatod? A színpad α látószögének változását is figyeld meg!
3. kérdés
A színpad vonalától való távolság és a látószög kapcsolatát egy függvénnyel ábrázolhatjuk. Az „α(x) elméleti” jelölőnégyzetbe tett pipa után, ha a P-t mozgatod, akkor kirajzolódik a színpad vonalától való távolság-látószög függvény néhány pontja.
4. kérdés
Vezesd végig a P pontot a teljes oldalpáholyon, és megjelenik még két jelölőnégyzet. A „α(x) kísérleti” kirajzolja a teljes függvénygrafikont.
5. kérdés
Hogy segít az α(x) függvény megtalálni a legjobb helyet?
6. kérdés
A α(x) függvény mely pontja adja meg a megoldást?
7. kérdés
Matematikai ismereteid alapján hogy határozható meg egy függvény maximuma?
8. kérdés
A „α’(x)” kirajzolja a deriváltfüggvényt. Ahol ennek zérushelye van, és ott a derivált értéke pozitívból negatívba megy át, onnan látszódik a színpad a legnagyobb szögben.
9. kérdés
A színpad méretének változtatásával figyeld meg, hogyan változik a legjobb oldalpáholy helye!
A képlet levezetése
Az α(x) függvény felírása, deriválása és szélsőérték-helyének megkeresése:
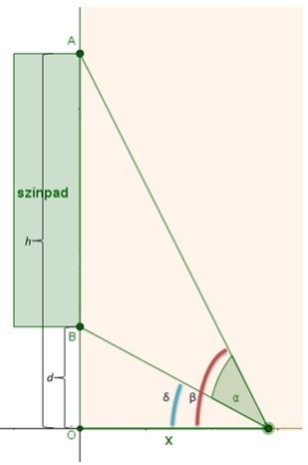
Jelöljük az ábra szerint a szögeket és szakaszokat (d > 0 és h > 0 állandó,
h > d, x > 0)!
Ábra a képlet levezetéséhez
Képlet levezetése