10-1 Classwork (Inverses)

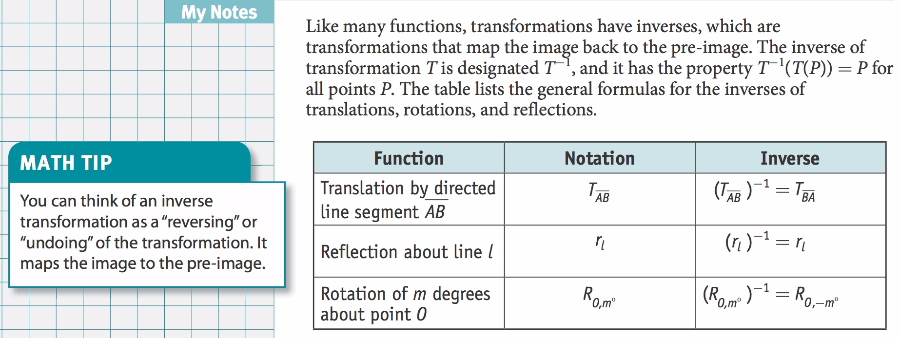
1. Describe what an inverse transformation is in your own words

2. Compare and contrast the inverse for translations, reflection, and rotations. (what stays the same for each pair, what is different between the notation and the inverse in each pair.)

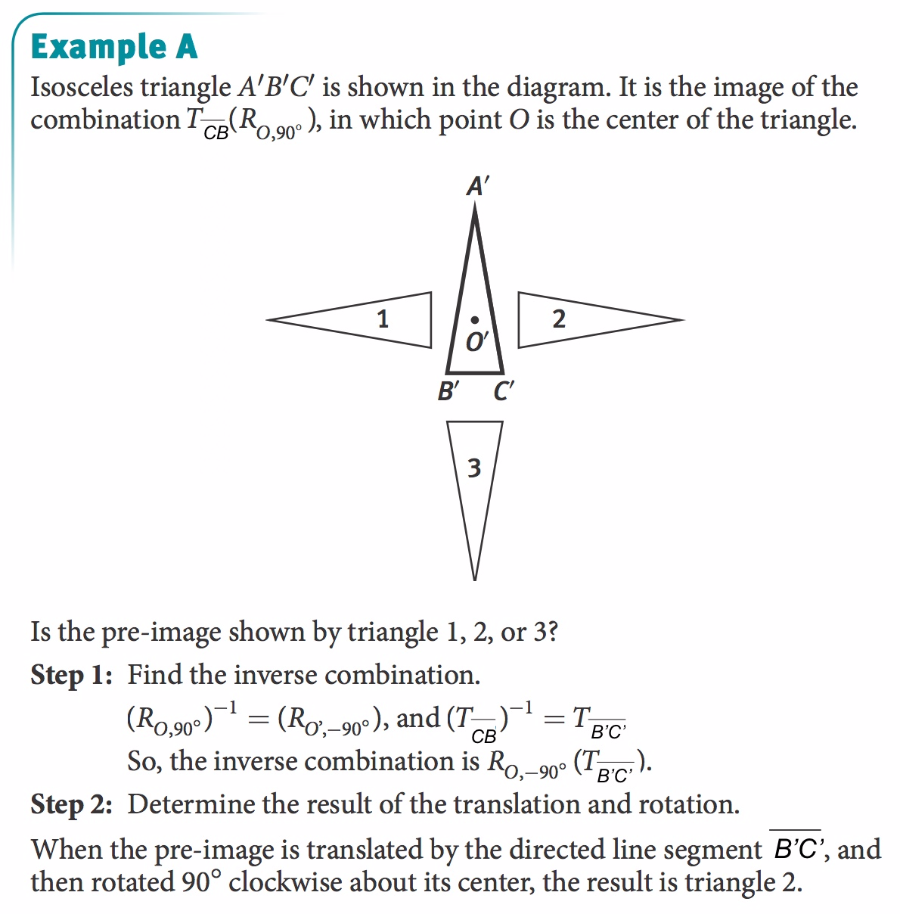
3. Summarize the problem above: Write the general steps you would take to find the inverse of a COMPOSITION OF TRANSFORMATIONS

4. Find a composition that maps triangle 1 to triangle A'B'C'.

5. What would be the inverse of that composition (in #4)?

6. Find a composition that maps triangle 3 to triangle A'B'C'.

7. What would be the inverse of that composition (in #6)?

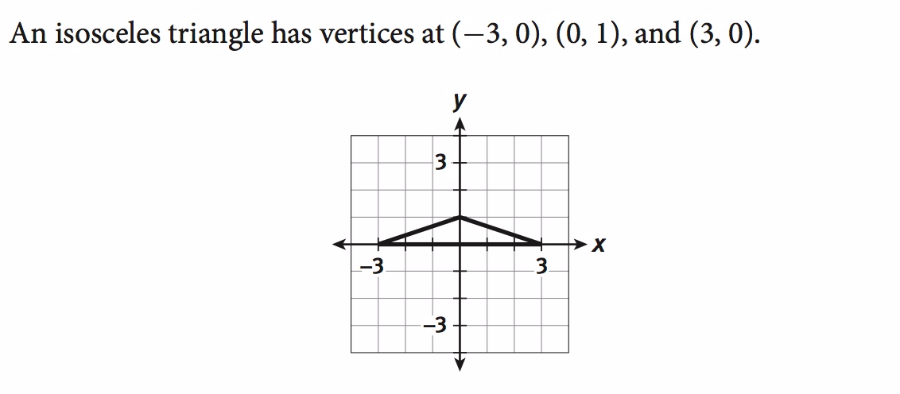
8. We performed the composition T_(0,2)(R_O,180) on this triangle in the last worksheet. What would the inverse of that composition be?

9. We also said that T_(0,2)(R_O,180) is equivalent to r_y=1. What is the inverse of that reflection?