moltiplicazione e divisione

Moltiplicazione del moltiplicatore A per il moltiplicando B e divisione del dividendo B per il divisore A. Inverso di A.

La moltiplicazione a coefficienti reali

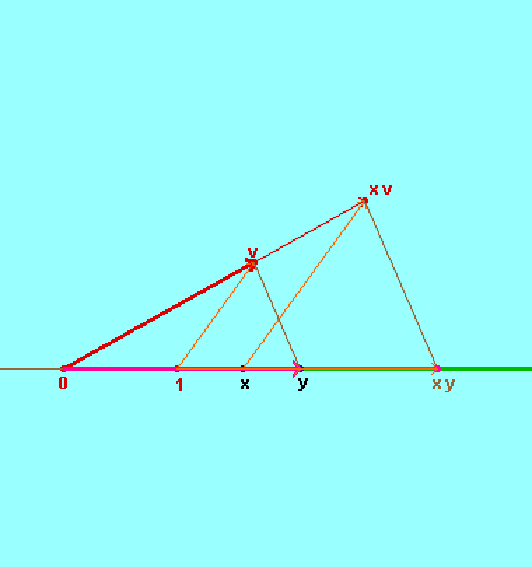
graficamente la moltiplicazione a coefficienti reali viene realizzata tramite la regola delle parallele di Talete: il segmento congiungente x con xv è parallelo al segmento congiungente 1 con v Osserviamo esplicitamente, come nel caso della precedente "regola del parallelogramma" per l'addizione, che si tratta di una regola "grafica" (che quindi rientra nell'ambito pratico del "disegno"), in quanto riguarda il modello concreto, non la teoria matematica che lo descrive
matematicamente, quindi "formalmente", definiamo la moltiplicazione a coefficienti reali nel modo seguente: la moltiplicazione a coefficienti reali (detta anche, per un motivo che sarà chiaro in seguito, moltiplicazione lineare) è un'operazione da RxC a C, che porta R⁺ x R⁺ in R⁺ (ossia: il prodotto di numeri positivi è un numero positivo) e che gode delle seguenti 4 proprietà (assiomi della moltiplicazione a coefficienti reali, o assiomi moltiplicativi):
neutralità dell'uno: 1v = v
associatività dei moltiplicatori: (xy)v = x(yv)
distributività a sinistra (o distributività del moltiplicatore): x(v+w) = xv + xw
distributività a destra (o distributività del moltiplicando): (x+y)v = xv + yv

Addizione e moltiplicazione lineare vengono usate insieme per costruire espressioni dette combinazioni lineari: esse sono tutte le somme di prodotti, del tipo xv + yw. Approfondimenti: 1) A partire da questi quattro assiomi si possono dimostrare vari teoremi sulla moltiplicazione a coefficienti reali: propriètà di assorbimento dello zero, associazione del segno meno, sottomultipli ottenuti come prodotto, ecc. 2) La moltiplicazione in R: quando v appartiene all'asse reale, xv diventa ovviamente il prodotto fra due numeri reali; continua a valere la regola grafica di Talete, ma usando un punto fuori di R come ponte per il trasporto parallelo. (Vedi la figura nel riquadro successivo) La moltiplicazione in R ha specifiche proprietà (deducibili dai quattro assiomi sui numeri reali):

- monotonicità: se x > 0 e y < y', allora xy < xy' (segue subito dalla distributibità a sinistra e dal fatto che la moltiplicazione porta fattori positivi in un prodotto positivo) - archimedeità: dati due numeri reali positivi r e x, esiste un numero naturale n tale che x < nr

- commutatività della moltiplicazione in R: xy = yx ( visualizzazione grafica ) ( vedi anche qui )

- invertibilità della moltiplicazione in R^* = R - {0}: per ogni x numero reale non nullo esiste un numero reale non nullo, indicato con 1/x, tale che x(1/x) = 1. Il numero 1/x è detto inverso (o reciproco) di x. A questo punto, definendo y/x := (1/x)y (rapporto fra y e x), si ha: x(y/x)=x((1/x)y)=(x(1/x))y=1y=y.

( Applicazioni grafiche: [1] [2] )

moltiplicazione e divisione

Moltiplicazione di due numeri reali

Nuove risorse

Scopri le risorse

Scopri gli argomenti