Voorbeeld + opgaven 40 en 41
Voorbeeld: helling van een functie in een punt kunt berekenen
Gegeven is de functie f(x) = x2. Bereken zonder de grafische rekenmachine het differentiaalquotiënt van deze functie voor x = 3. Stel met behulp daarvan een vergelijking op van de raaklijn aan de grafiek van f voor x = 3.
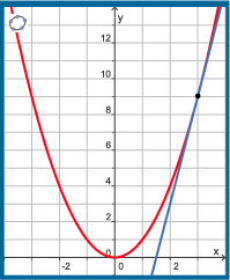
Oplossing:
Het differentiequotiënt van f op het interval [3,3+h] is:
(mits h ≠ 0).
Als h de waarde 0 nadert, dan nadert 6+h het getal 6. Dit is het differentiaalquotiënt van f voor x = 3.
Met de grafische rekenmachine kun je controleren dat het differentiaalquotiënt inderdaad 6 is voor x = 3.
Het getal 6 is ook het hellingsgetal van de raaklijn aan de grafiek van f voor x = 3. Deze raaklijn is een rechte lijn en heeft daarom een vergelijking van de vorm: y = 6x + b.
Omdat f(3) = 32 = 9, gaat deze raaklijn door het punt (3,9). Dit betekent dat: 9 = 6⋅3 + b en dus geldt: b = −9.
De vergelijking van de gevraagde raaklijn is y = 6x − 9.
Opgave 40
In het voorbeeld zie je de functie f(x) = x2.
Stel zonder hulp van de grafische rekenmachine de formule op van de raaklijn aan de grafiek van f voor x = -2.
Opgave 41
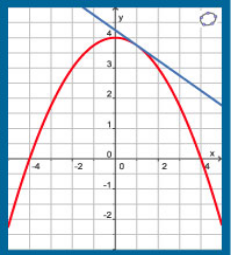
Hieronder zie je de grafiek van de functie f(x) = 4−0,25x2 op het domein [-5,5].
a. Bereken het differentiequotiënt van f op het interval [1,1+h].
b. Welke hellingsgetal heeft de raaklijn aan grafiek van f voor x = 1?
c. Dit hellingsgetal is tevens de richtingscoëfficiënt van de raaklijn aan de grafiek voor x = 1. Stel een vergelijking van die raaklijn op.