Wendepunkte
Im letzten Kapitel haben wir festgestellt, dass es bei der Funktion einen Punkt gibt, an dem die zweite Ableitung Null ist und an dem es "einen Moment lang" geradeaus geht.
Ein solcher Punkt heißt Wendepunkt der Funktion, weil dort eine Links- in eine Rechtskurve übergeht oder umgekehrt. Allerdings muss man aufpassen: Ähnlich wie sich bei den Hoch- und Tiefpunkten zusätzlich die Sattelpunkte in die Liste der Kandidaten geschlichen hatten, gibt es auch hier "Blindgänger". Man muss zusätzlich prüfen, ob die zweite Ableitung einen Vorzeichenwechsel von + nach - oder umgekehrt hat, denn nur dann ist es auch ein Übergang von einer Kurvensorte in die andere.
Klarer wird's an zwei Beispielen:
Bsp: Wendepunkt
Überprüfen des Vorzeichenwechsels:
Zwei praktische Zahlen links und rechts von 0 werden eingesetzt (hier -1 un d1):
und . Das heißt es gibt einen Vorzeichenwechsel und damit einen Übergang von einer Kurvenart in die andere. Bei x=0 ist also ein Wendepunkt. Seine y-Koordinate ist . Der Wendepunkt laute also: .
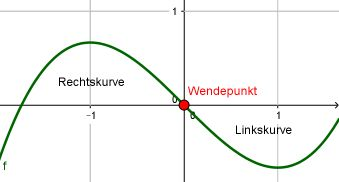
Bsp: "Blindgänger"
Überprüfen des Vorzeichenwechsels:
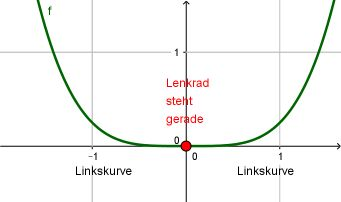
und . Das bedeutet, wir haben vor und nach der Stelle x=0 jeweils eine Linkskurve, die an der Stelle x=0 nur mal kurz unterbrochen ist. Es gibt dort also keinen Wendepunkt.
Wie sieht das dann aber aus? Du kannst es dir so vorstellen: Du fährst mit dem Auto eine Linkskurve, die immer schwächer wird, bis das Lenkrad dann irgendwann gerade steht. Und dann geht die Linkskurve aber sofort wieder weiter (Du drehst das Steuerrade also erneut nach links). So sieht diese Funktion aus: