Pm - Matrixmultiplikation
Damit zwei Matrizen und miteinander multipliziert werden können, muss die Matrix so viele Spalten haben, wie die Matrix Zeilen hat.
Es muss erfüllt sein, sonst können die Matrizen nicht miteinander multipliziert werden.
Zu beachten ist, dass die Matrixmultiplikation nicht kommutativ ist!
In der Regel gilt:
Die Ergebnismatrix der Multiplikation hat immer so viele Zeilen, wie die erste Matrix und so viele Spalten wie die zweite Matrix.
Die einzelnen Elemente der Ergebnismatrix werden berechnet, indem die jeweiligen Elemente der Ausgangsmatrizen multipliziert und die Teilprodukte addiert werden.
Das klingt sehr kryptisch, ist aber nicht schwer.
In der Beispielaufgabe wurde bereits eine Matrixmultiplikation durchgeführt und nachgeschlagen werden.
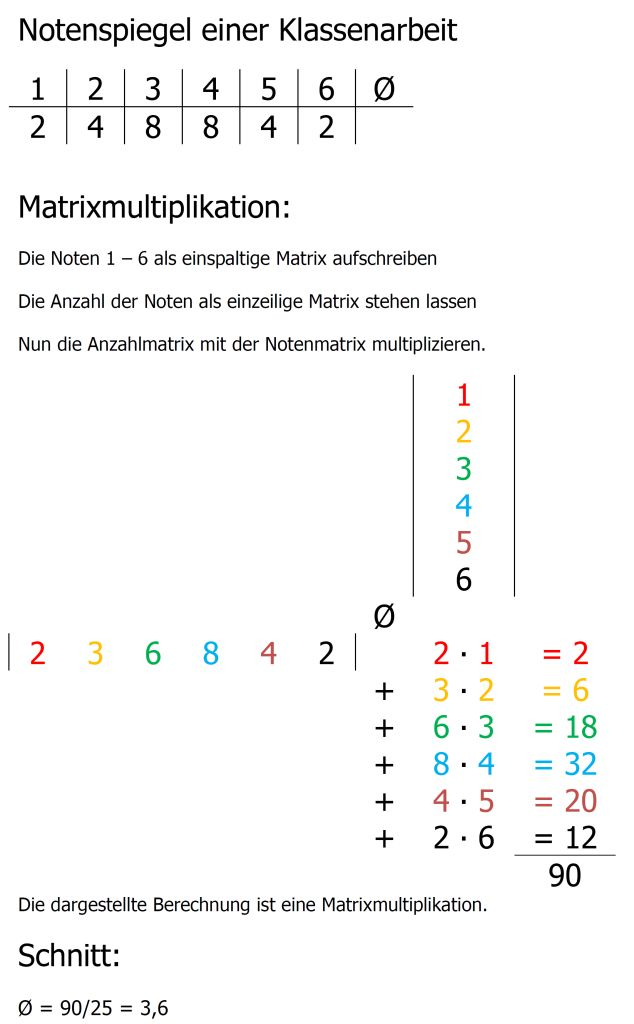
Veranschaulichen lässt sich die Berechnung der einzelnen Matrixelemente mit der Berechnung des Notenschnitts einer Klassenarbeit. Um den Notenschnitt zu Berechnen, wird eine Matrixmultiplikation durchgeführt.
(Um den Schnitt zu erhalten muss das Matrixprodukt noch durch die Anzahl der Schüler und Schülerinnen dividiert werden.)