Infoblatt Lineare Funktionen 2024 FRG
Da die Variable x in der Gleichung -0,5x +y = 3 nur in der ersten Potenz (x1) vorkommt, bezeichnet man sie als lineare Gleichung.
Durch Auflösen dieser linearen Gleichung nach der Variablen y, erhält man die Normalform der linearen Funktion: f : y = 0,5x +3 .
Da bei Funktionen der Wert der Variablen y immer vom Wert der Variablen x abhängt,
bezeichnet man x als unabhängige Variable oder Argument (Abzissenwert) und
y entsprechend als abhängige Variable oder Funktionswert (Ordinatenwert).
Die Menge der x-Werte, die durch die Funktion f abgebildet werden, bezeichnet man als
Definitionsmenge Df der Funktion.
Entsprechend bilden alle möglichen y-Werte (Funktionswerte), die sich durch Einsetzen von x in den
Funktionsterm f(x) ergeben, die Wertemenge Wf der Funktion.
Die lineare Funktion f : y = 0,5x +3 lässt sich im Koordinatensystem graphisch als Gerade mit dem positivem Steigungsfaktor (englisch: slope) m = 0,5 und dem y-Achsenabschnitt (englisch: intercept)t = 3 darstellen.
Der Steigungsfaktor m lässt sich mit Hilfe des eingezeichneten Steigungsdreiecks ablesen.
Auf der Gf liegen alle Punkte P ( x ; y ), die den Funktionsterm f erfüllen. (f(x) = 0,5x +3)
Durch Parallelverschiebung dieser Geraden in den Koordinatenursprung (Koordinatensystem – Mittelpunkt) ergibt sich die sogenannte Ursprungsgerade g : y = 0,5x
Wie nennt man alle Geraden mit verschiedenem m aber gleichem t?
Wie nennt man alle Geraden mit verschiedenem t aber gleichem m?
Im Allgemeinen gilt:
Jede Gerade im Koordinatensystem, die nicht parallel zur y-Achse ist, ist der Graph einer Funktion mit einer Funktionsgleichung der Form
f(x)= y = m . x + t
Funktionen mit solch einer Funktionsgleichung werden lineare Funktionen genannt.
Ein positives t entspricht einer Verschiebung des Graphen der proportionalen Funktion f(x)= y = m . x entlang der y-Achse um t - Längeneinheiten nach oben.
Ein negatives t entspricht einer Verschiebung des Graphen der proportionalen Funktion f(x)= y = m . x entlang der y-Achse um t-Längeneinheiten nach unten.
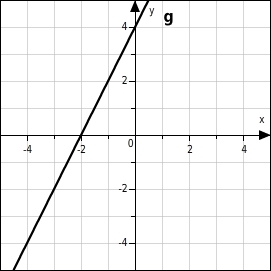
Gib nun die Funktionsgleichung zu dem nachfolgendem Graphen an.