Model from an image
One of the ways in which you can do the Maths internal assessment is looking for a Maths model of something in real life, in this case we will use a mixture of Maths and architecture because we are going to look for a model that fits the roof of aeropuerto internacional de Carrasco. So first create a word document with the title Maths Project "Aeropuerto de Carrasco" and create an introduction explaining what are you going to do. As we said a Maths internal is not only doing calculations so you must create an introduction explaining that you are going to find a model for the roof of the airport maybe because you want to see if it was done following a maths model or maybe because you are fascinated about architecture but you must find a reason to do so in other to give coherence to your internal assessment. Create the introduction explaining what you are going to do, find an aim for that to be done. Introduce a picture of the aeropuerto, give some information about it. Then continue below...
In the following applet:
Insert 7 points in the roof of the aeropuerto. You must use the tool  (firs click on the picture, one example is done)
Then looking at the x and y coordinates in the algebra view copy them in the spreadsheet alongside.
The x-coordinate in column A and the y-coordinate in column B. (an example has been done)
(firs click on the picture, one example is done)
Then looking at the x and y coordinates in the algebra view copy them in the spreadsheet alongside.
The x-coordinate in column A and the y-coordinate in column B. (an example has been done)
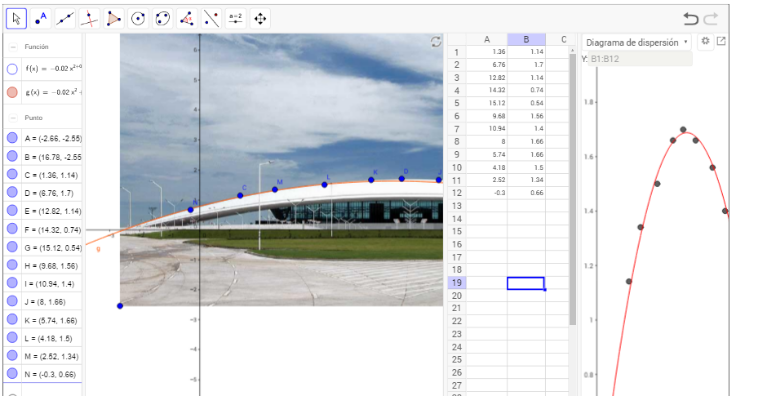
 (two variable analysis)
Select the regression model that you think will be the best fit for this roof.
Now introduce the algebraic model that GeoGebra found to check if the model really fits. Be careful to input the model as a function: use instead of y=.
(two variable analysis)
Select the regression model that you think will be the best fit for this roof.
Now introduce the algebraic model that GeoGebra found to check if the model really fits. Be careful to input the model as a function: use instead of y=.You should get something similar to this.
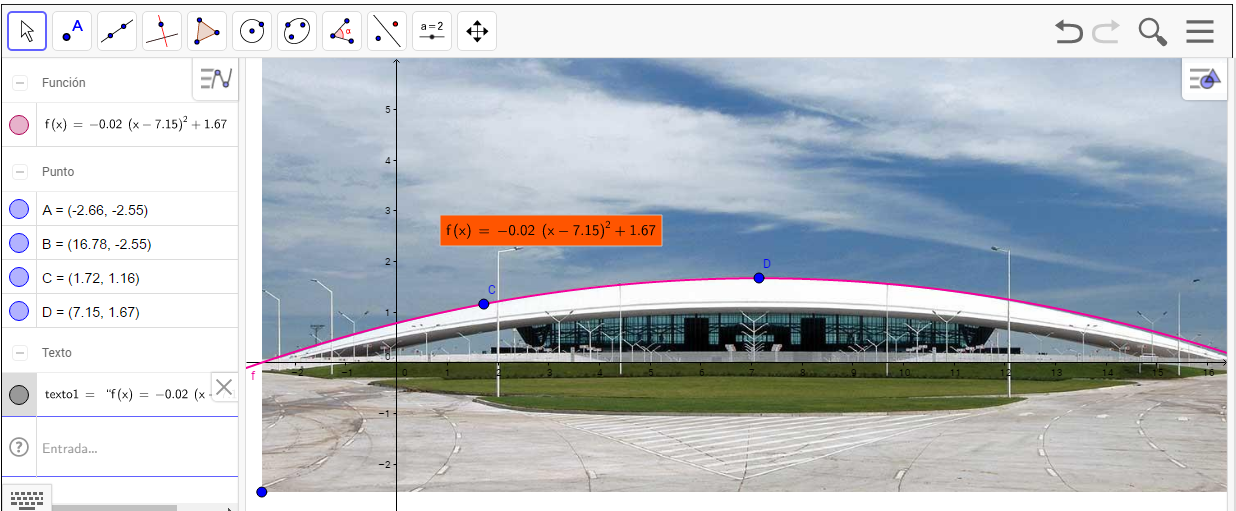
Obviously there is a way of getting the model that does not requires the software. Once we have some coordinates of the points we can find the model by some algebraic means. For example if we think of a third degree function we could have used simultaneous equations to obtain the coefficients. Also we can use the vertex form of the equation. Estimate the vertex, fin any other point and we one simple equation we have to model. Remember the vertex form is being and the coordinates of the vertex. An example of this: Estimated vertex: (7.15,1.67) Another point in the graph: (1.72, 1.16) Substitute vertex coordinates: Substitute coordinates of point C: Solve equation to get :
This model looks like this.
Continue the WORD document: Explain the equations or the process you did to find the model, put every equation in maths format using the equation editor. Put a picture to show how you model fitted the roof. Be sure to include all details about the process.
More maths in the internal.
To include and use in a very good way some more of the maths seen in this course we are going to use integrals to find the area under this curve. This obviously must be justified in the aim of the project. For example we are going to calculate the area to see how many square meters of glass will be needed to close the front of the airport. To calculate the integral we must find the roots of the function because in this case, the picture was uploaded in a clever way fitting it in the x-axis so now calculations are a little bit more easy. In the input bar write: 'roots' or 'raíces' depending on the language. Then introduce the required data and you will have the roots. (In the real internal assessment you will have to do this algebraically.) Then in the input bar write: 'integral' and complete the data required. You will now notice that GeoGebra has calculated the area below the curve. So we can use that data in our project. (Latter in this course you will be able to calculate this algebraically with no need of this software. Continue the WORD doc: Complete the word with this picture, the new calculations, why was this done? what it means? how this helps you to do the project, etc. Now think about the scale of this project. Are you using the real scale? how can you arrange it to fit reality? Create a final conclusion of what you did so far, does this model present some limitations? which limitations? can it be improved? how? did you applied maths? how?