ÁREA E VOLUME DA ESFERA
ÁREA DA SUPERFÍCIE ESFÉRICA
Figura 2 - CÁLCULO DA ÁREA DA SUPERFÍCIE ESFÉRICA
VOLUME DA ESFERA
Segundo o PRINCÍPIO DE CAVALIERI, dois sólidos de mesma altura tem volumes iguais quando as áreas das secções obtidas sobre esses sólidos, por um plano paralelo a suas bases têm o mesmo valor. Dessa forma, o volume de uma semi-esfera (meia esfera) é igual ao volume de um cilindro menos o volume de um cone, ambos com altura h e raio da base iguais ao raio R da esfera. Observe a animação da figura abaixo, onde temos uma semi-esfera de raio R = 2 .
Figura 3 - VERIFICAÇÃO DO PRINCÍPIO DE CAVALIERI
Como temos h = R, então Portanto, podemos concluir que o volume da esfera será dado por:
Figura 4 - CÁLCULO DO VOLUME DA ESFERA
ATIVIDADE 5
(Imed 2016) Uma bola maciça, totalmente vedada, em formato de uma esfera perfeita, de diâmetro igual a 2 metros, foi lançada em uma piscina, de base retangular com dimensões medindo 5 metros e 12 metros e com água até a altura de 1,2 metros. Sabendo que a bola ficou completamente submersa pela água, quantos metros o nível da água se elevará?
ATIVIDADE 6
(Enem PPL 2015) Um artesão fabrica vários tipos de potes cilíndricos. Mostrou a um cliente um pote de raio de base a e altura b. Esse cliente, por sua vez, quer comprar um pote com o dobro do volume do pote apresentado. O artesão diz que possui potes com as seguintes dimensões:
- Pote I: raio a e altura 2b
- Pote II: raio 2a e altura b
- Pote III: raio 2a e altura 2b
- Pote IV: raio 4a e altura b
- Pote V: raio 4a e altura 2b
O pote que satisfaz a condição imposta pelo cliente é o
ATIVIDADE 7
(Cefet-MG 2014) Um artesão resolveu fabricar uma ampulheta de volume total V constituída de uma semiesfera de raio 4 cm e de um cone reto, com raio e altura 4 cm, comunicando-se pelo vértice do cone, de acordo com a figura abaixo.
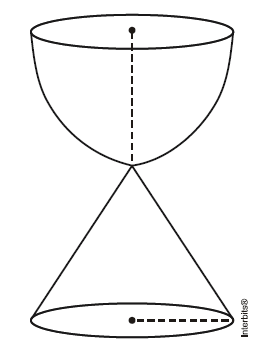
Para seu funcionamento, o artesão depositará na ampulheta areia que corresponda a 25% de V. Portanto o volume de areia, em cm³, é