Función Biyectiva
1.8 Función biyectiva
Introducción
Una función f es biyectivasi es al mismo tiempo inyectiva y sobreyectiva. Es decir, si todo elemento del conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde (condición de función sobreyectiva) y todos los elementos del conjunto inicial X tiene una única imagen en el conjunto final Y (condición de función inyectiva).
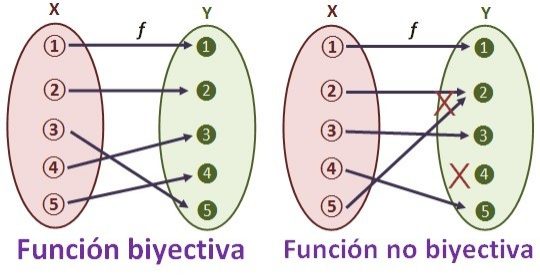
Teóricamente una función es biyectiva si:
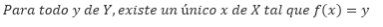
Supuesto de aplicación
Constantemente en la vida diaria se está en contacto con funciones biyectivas, por ejemplo:
- En esta imagen podemos observar que en cada inclinación que se vea de este tipo, como rampas, una
- También se ve de una forma más ejemplificada cuando se conectan los cables de una televisión a tu
¿Qué podemos ver en el applet?
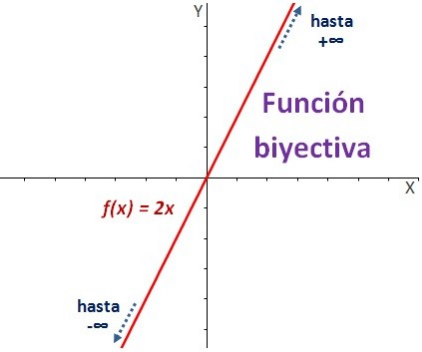
Podemos ver a Superman volando, su vuelo describe a una función Biyectiva por
definición.
1.- A cada distancia en el suelo le corresponde una altura.
2.- A cada altura le corresponde por lo menos una posición en el suelo.
¿Cómo funciona el applet?
El applet tiene un deslizador automático que aumenta la altura del vuelo, para poder ver su
distancia del punto de partida hasta donde se proyecta la sombra. Este deslizador lo podemos mover de manera manual.