Axonometrie
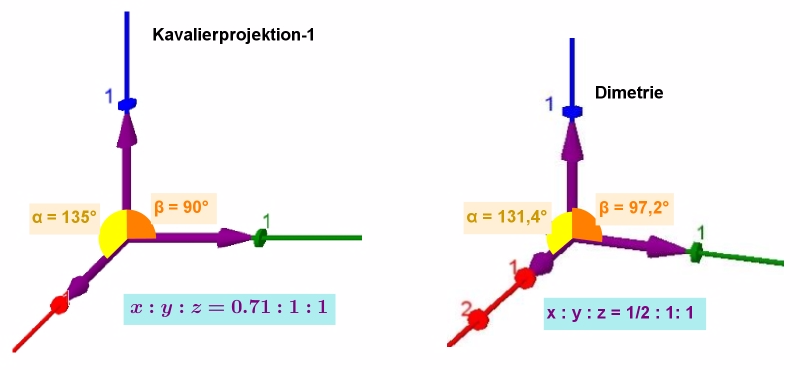
Bei den Projektionen 3D -> 2D ist das ebene Bild der drei Einheitsvektoren, die im Raum ein orthogonales Dreibein bilden, von besonderer Bedeutung. Das ebene Dreibein kann man in der Bildebene durch die gegenseitige Lage der Bilder der Einheitsvektoren und die Proportionen auf den Achsen charakterisieren. Dann spricht man von Axonometrie. Dies ist der klassische Ansatz der Darstellenden Geometrie aus Sicht der Bildebene/ des 2D-Zeichenblatts, das 'Messen entlang der Achsen' im Zeichenblatt. Zwei Beispiele sind unten zu sehen. Man kann sich das anschaulich so vorstellen, dass separat zum dreidimensionalen Objekt ein Zeichenblatt mit einem eigenen x'y'-Koordinatensystem auf einem Tisch liegt und in diesem Zeichenblatt nun das Bild des Objektes konstruiert werden soll.
Jedes ebene Dreibein legt eine Projektion fest. Dies ist der Satz von Pohlke.
Eine anderer Ansatz wäre die Angabe von Projektionsrichtung und Bildebene (quasi der Bildschirm), dies ist die Sicht der Analytischen Geometrie. Und ein weiterer, dem entsprechender Ansatz aus der Linearen Algebra wäre die Angabe von Projektionsmatrizen, wo in den Spalten die Bilder der Einheitsvektoren stehen.
In GeoGebra wird bei der schrägen Parallelprojektion zunächst über die Blickrichtung (mittels Icons) die Bildebene festgelegt und dann kann man noch Winkel und (Verkürzungs-)Faktor definieren.
Diese Projektionsparameter sind in GeoGebra etwas versteckt und schwer zu entdecken. Man findet sie nach rechtem Mausklick in die 3D-Grafik unter 3D Grafik .../ Projektion/Schräg.
- Anmerkung: Die axonomischen Parameter sind vor allem in der Darstellenden Geometrie gebräuchlich, werden aber nicht in gleicher Weise in GeoGebra genutzt. Der GeoGebra-Parameter Winkel kann ggf. daraus berechnet werden und den GeoGebra-Parameter Faktor können wir daraus entnehmen.
Eingabe axonometrischer Parameter für die schräge Parallelprojektion