Tečna ke grafu funkce
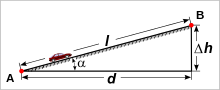
Spád – stoupání
Stoupání resp. klesání vyjadřuje geometrický sklon úseku cesty (silnice, kolejí apod.). Je to poměr mezi přírůstkem resp. úbytkem výšky a odpovídající vodorovnou vzdáleností. Rovná se tangens úhlu stoupání resp. klesání, což je úhel mezi vodorovnou rovinou a cestou. Na dopravní značce A5b - Nebezpečné stoupání je udáváno v procentech.
Je dána parabola jako graf kvadratické funkce y = x2. V bodě T sestrojte tečnu.
Intuitivně chápeme tečnu jako limitní případ sečny, kdy dva body A, T splynou. Pro výpočet její směrnice (spádu) použil Gottfried W. Leibniz (1646–1716) nekonečně malé veličiny dy, dx.
Tečnu definoval Leibniz jako přímku, která prochází dvěma body křivky, které jsou nekonečně málo od sebe vzdáleny. Při výstavbě své teorie se opíral o princip spojitosti, kdy veličiny, které se liší o nekonečně malou hodnotu, můžeme považovat za sobě rovné. Podobně; veličina, která se změní o nekonečně malou veličinu je považována za konstantu.
Problémem je, že Leibnizovi (a s ním i dalším průkopníkům - Newton, Euler) chybí přesná definice nekonečně malé veličiny dx. Není přímo řečeno, že nekonečně malá veličina je nula, v konkrétních případech se za ni ale považuje. Například mocniny a součiny jsou zanedbávány, ale je dovoleno jí dělit. Jinak jsou ji připisovány vlastnosti, jaké mají všechna čísla. Je ale menší než libovolná konečná veličina.
Přesnější matematická formalizace přišla až o století pozdějí, s pojmem limita (L'Hospital, d'Alembert, Cauchy a Bolzáno).
Sledujte změnu směrnice tečny při změně polohy červené šipky.
Pro zapsání předpisu funkcí použijte nápovědu Functions and Operators.