Fracciones equivalentes y fracción irreductible
¿Qué son las fracciones equivalentes?
Dos fracciones son equivalentes cuando el resultado de las divisiones que representan (numerador dividido denominador) es el mismo.
Por ejemplo, las fracciones 5/2 (cinco medios) y 10/4 (diez cuartos) son equivalentes porque el resultado de dividir 5 entre 2 es el mismo que el de dividir 10 entre 4:
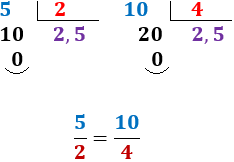

¿Cómo obtener fracciones equivalentes?
Observando las fracciones equivalentes del ejemplo (cinco medios y diez cuartos), podemos deducir que las fracciones equivalentes se obtienen multiplicando el numerador y el denominador por el mismo número (distinto de 0):
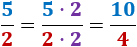
También, podemos dividir en lugar de multiplicar.
También, podemos dividir en lugar de multiplicar.
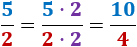
También, podemos dividir en lugar de multiplicar.
También, podemos dividir en lugar de multiplicar.¿Cómo saber si dos fracciones son equivalentes?
Si dos fracciones son equivalentes, entonces el resultado de la división numerador entre denominador es el mismo. Por tanto, una opción es calcular las divisiones.
También, podemos pensar si existe un número que al multiplicarlo en el numerador y en el denominador de una de las fracciones proporcione la otra fracción. Otra opción es escribir que las fracciones son iguales y operar en la igualdad para comprobar si realmente lo son.
Por ejemplo, comprobamos si las fracciones 12/22 y 3/2 son equivalentes:
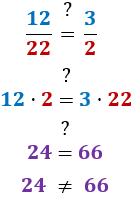
Las fracciones no son equivalentes porque 24 no es igual a 66.
Las fracciones no son equivalentes porque 24 no es igual a 66.
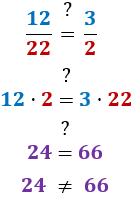
Las fracciones no son equivalentes porque 24 no es igual a 66.
Las fracciones no son equivalentes porque 24 no es igual a 66.¿Cuándo es irreductible una fracción?
Se conviene, por comodidad, escoger siempre la fracción que tiene los números más pequeños posibles. Esta fracción se denomina irreductible.
Un fracción es irreductible cuando el máximo común divisor (M.C.D.) del numerador y del denominador es 1.
Por ejemplo, la fracción 15/6 no es irreductible porque el M.C.D. de 15 y de 6 es 3. En cambio, el M.C.D. del numerador y denominador de la fracción equivalente 5/2 es 1. Por tanto, la fracción irreductible de 15/6 es 5/2.
Cuando una fracción es irreductible, no existe ningún número que sea divisor común del numerador y del denominador y, por tanto, no hay fracciones equivalentes cuyos números sean más pequeños.
¿Cómo encontrar la fracción irreductible?
Un forma de hacerlo es dividir el numerador y el denominador entre su M.C.D.
Por ejemplo, simplificamos la fracción 180/270 para calcular la fracción equivalente irreductible:
Las descomposiciones del numerador y del denominador son
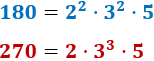
El M.C.D. es el producto de los factores comunes al menor exponente:
El M.C.D. es el producto de los factores comunes al menor exponente:
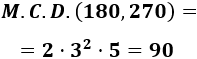
Dividimos en la fracción entre 90:
Dividimos en la fracción entre 90:
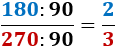
La fracción 2/3 es irreductible.
La fracción 2/3 es irreductible.
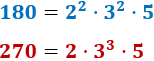
El M.C.D. es el producto de los factores comunes al menor exponente:
El M.C.D. es el producto de los factores comunes al menor exponente:
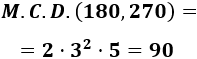
Dividimos en la fracción entre 90:
Dividimos en la fracción entre 90:
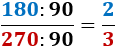
La fracción 2/3 es irreductible.
La fracción 2/3 es irreductible.Enlaces:
- Fracciones equivalentes y fracción irreductible
- Potencias (propiedades y ejercicios)
- Teorema de Pitágoras (con problemas resueltos)
- Ecuaciones de primer grado explicadas
- Problemas resueltos de ecuaciones
- Sistemas de ecuaciones (métodos)
- Problemas resueltos de sistemas de ecuaciones
- Ecuaciones de segundo grado resueltas
- Ecuaciones bicuadradas resueltas
- Problemas de progresiones o sucesiones
- Problemas resueltos de mcm y mcd
- Problemas resueltos de trigonometría (seno, coseno y tangente)
- Problemas de movimiento rectilíneo uniforme (MRU)
- Ecuaciones exponenciales resueltas
- Integrales resueltas (directas, por sustitución y por partes)
- Números complejos o imaginarios
- Problemas y Ecuaciones
- Logaritmos
- Teorema de Pitágoras online
- Calculadoras de porcentajes online