Funções
Introdução
- Função se define como uma relação estabelecida entre dois conjuntos A e B, onde exista uma associação entre cada elemento de A com um único de B através de uma lei de formação.
- Entre os estudos das funções, temos: função do 1º grau, função do 2º grau, função exponencial, função modular, função trigonométrica, função logarítmica e função polinomial.
- Dê uma olhada nos tipos de funções abaixo:
Função Afim
Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados e a
0.
Na função f(x) = ax + b, o número a é chamado de coeficiente de x e o número b é chamado termo constante.
Função quadrática
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a 
0.
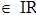Para que o conceito de função fique claro adotamos a notação de uma função f(x) = |x|, como sendo:
Sendo que o gráfico de f(x) = |x| é semelhante ao gráfico de f(x) = x, sendo que a parte negativa do gráfico será “refletida” sempre para um f(x) positivo.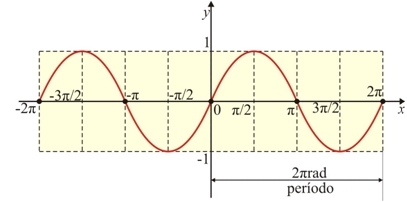
Função exponencial A função exponencial é aquela em que a variável é um expoente. Matematicamente, ela é definida como f de R em R, tal que f(x) = ax, em que a ϵ R, a > 0 e a ≠ 1. O gráfico dessa função é uma curva obtida ao encontrar alguns pares ordenados que pertencem à função e ao desenhar essa curva que passa por eles.
Função Raiz
A função raiz é definida pela fórmula:
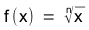f(x) = imagem
x = domínio
n = índice
Podemos reescrever da seguinte forma:
f(x) = x1/n
- f(x) = imagem;
- 1/n = expoente. O n sempre deve ser positivo, ou seja, um número natural;
- x = domínio. O x pode ser positivo ou negativo. Para x positivo, n pode ser ímparou par; para x seja negativo, n poderá ser somente ímpar. Essa restrição está relacionada com o fato de não existir raiz quadrada para n par e x negativo.