IM1.5.7 Calculator Skills
See an equation as two functions
Let's look at our opening problem again: Think about this problem as two functions, one for the left side and one for the right side: and . Follow the directions for solving this equation on your calculator, and enter the solutions below.
Keystrokes

Graphed equations

Solving with a table

Solving with a graph

Try it on your own
Equation: 1. Write the two functions you will graph on your calculator. 2. Write the intersection points of the two functions. 3. The original equation is true when x= _____ or _____.
4. Find the solutions to the equation
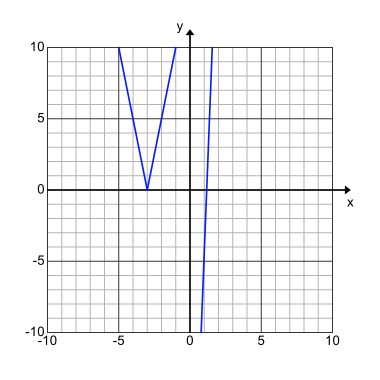
5. The graphs of f, a function that involves taking an absolute value, and g a linear function, are shown above. Both functions are defined over all real values for x. Tami concluded that the equation f(x)=g(x) has no solution. Do you agree or disagree? Explain your reasoning.