Padovan meetkundig
- Author:
- chris cambré
- Topic:
- Triangles
Fibonacci meetkundig
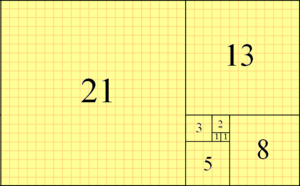
De rij van Fibonacci kan je grafisch voorstellen als aan elkaar aansluitende vierkanten waarvan de zijden overeenkomen met de getallen uit de rij.
Padovan meetkundig
De rij van Padovan kan je op een analoge manier voorstellen, maar dan met aan elkaar aansluitende gelijkzijdige driehoeken.
tweede vormingswet
In het applet zie je hoe de rij opgebouwd wordt vanuit de vormingswet Pn=Pn-2+Pn-3.
Tegelijk voldoet de rij ook aan de gelijkheid Pn=Pn-1+Pn-5. Zo is:
| 2=1+1 | maar ook | 2=1+1 |
| 3=2+1 | | 3=2+1 |
| 4=2+2 | | 4=3+1 |
| 5=3+2 | | 5=4+1 |
| 7=4+3 | | 7=5+2 |
| 9=5+4 | | 9=7+2 |
| 12=7+5 | | 12=9+3 |
| 16=9+7 | | 16=12+4 |
| 21=12+9 | | 21=16+5 |