Heptágono
Propiedades de un heptágono
Un heptágono tiene catorce diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono, 
; siendo el número de lados 
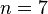, tenemos:
; siendo el número de lados 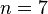, tenemos: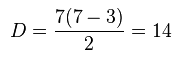
La suma de todos los ángulos internos de cualquier heptágono es 900 grados o 
radianes.
radianes.PASOS PARA LA CONSTRUCCIÓN DE UN HEPTÁGONO (en Geogebra)
1) Creamos una circunferencia (Centro y un punto de la circunferencia).
2) Trazar una recta que cruce la circunferencia en dos.
3) Luego en uno de los puntos se traza otra circunferencia.
4) Marcamos los puntos donde se intersecta la primera recta (C-D)
5) Después marcamos el segmento que unen a C y D.
6) En una de las intersecciones de dicha recta se traza una circunferencia y en el punto resultante de esta se traza otra, se repite el proceso hasta terminar la circunferencia inicial.
7) Los puntos (centro) de cada circunferencia se unen con segmentos entre dos puntos y vemos que se obtienen 7 rectas lo que forma el heptágono (inscrito en circunferencias)
Heptágono regular
En un heptágono regular, aquel cuyos lados y ángulos son iguales, los lados se unen formando un ángulo de aproximadamente 128,57º o exactamente 5π/7 radianes. Cada ángulo externo del heptágono regular mide aproximadamente 51,43º ó exactamente 2π/7 radianes.
El perímetro P de un heptágono regular puede calcularse multiplicando la longitud t de uno de sus lados por siete (el número de lados n del polígono).
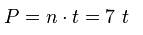
El área A de un heptágono regular con lados de longitud t sería:
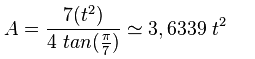
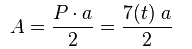
es la constante 
es la función 