Atividade 9: ÁREA DA SECÇÃO DADA PELO PLANO PERPENDICULAR A DIAGONAL DO CUBO

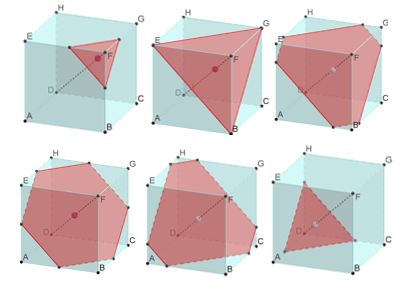
a)  Como você realizou esta construção? Descreva os passos utilizados.

b) Como são as formas das secções formadas?Descreva-as.   

c) Em algum momento a secção não é um polígono regular? Quando? Ilustre essa situação e descreva em que momento isto acontece.

d)  Como é a variação da área da seção, conforme a seção se afasta do vértice F do cubo?

e)  Exiba a vista 2D do plano de corte e determine qual a secção de maior área e quando isto acontece? 

f)     Construa o gráfico que representa a variação da área das secções na Janela de Visualização 2. Após, analise se a sua resposta para o item d e e corresponde ao encontrado. 

a)      Calcule a área da seção que corresponde ao maior triângulo equilátero formado. 

b)      Calcule a área da seção quando ela é o hexágono regular formado por pontos médios das arestas.