Kapitel
Dobrodošli v PROSTOR!
V Wikipediji piše: "Prostor je brezsnovna in neomejena entiteta v kateri so telesa, kjer se lahko gibljejo, in v kateri so pojavljajo dogodki. Po navadi pod prostorom razumemo trirazsežni prostor v fizikalnem smislu, v katerem imajo telesa relativno lego in smer. Sodobna fizika opredeljuje trirazsežni prostor skupaj s časom kot del neomejenega štirirazsežnega kontinuuma, prostor-časa. Matematika proučuje prostore v različnih razsežnostih, z različnimi povezanimi strukturami in z osnovnimi matematičnimi modeli. V osnovi je prostor pomemben za razumevanje fizičnega Vesolja, čeprav se nadaljujejo nesoglasja med filozofi ali je prostor sam po sebi entiteta, povezava med entitetami ali del pojmovnega ogrodja". Ali ti je vse jasno? Meni ne! Ali bi skupaj poskusili kaj več razumeti?
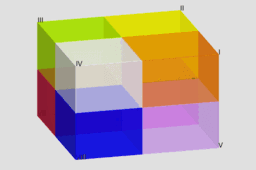
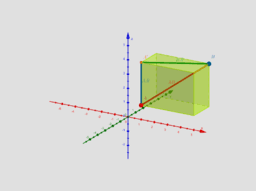
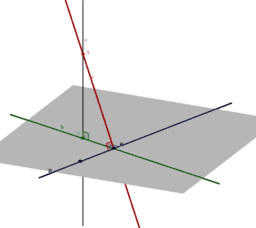
L1-L2 Spoznajmo pravokotni koordinatni sistem v prostoru! Od kvadrantov do oltantov!
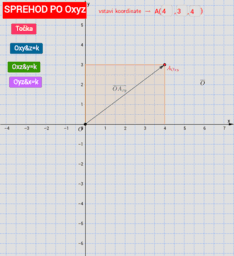
L3 Ali je prostor res tako različen od ravnine?
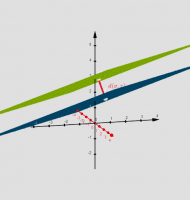
Ponovimo razdalje v ravnini (točka-točka, točka-premica, med vzporednima premicama) in poglejmo kaj je/so razdalja/e v prostoru (točka-točka, točka-ravnina, točka- premica, razdalja med vzporednima ravninama).
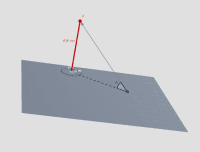
L4-L5-L6 Kaj je kot? V ravnini samo pogledamo in takoj nam je vse jasno! In v prostoru?
Odgovorili bomo na naslednja vprašanja:
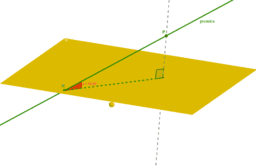
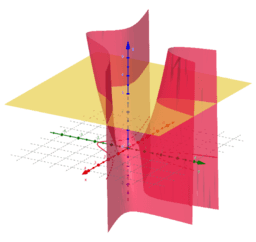
a) Kako določimo kot med premico in ravnino?
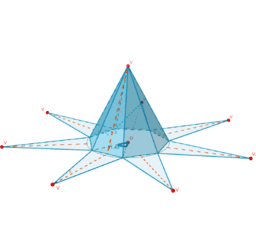
b) Povedali bomo kaj več o pravokotnosti v prostoru in povezali z nekaterimi že poznanimi lastnostmi piramide!
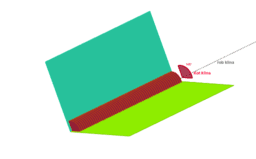
c) Kaj pa kot med dvema ravninama?
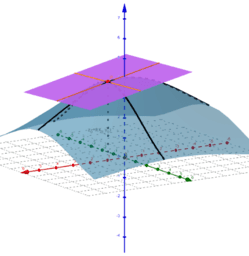
L7 Ali obstaja kaj sličnega stožnicam?
L8 Odgovorili bomo na vprašanja:
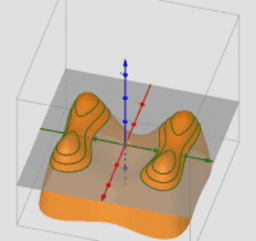
a) Ali je vsaka ploskev "graf" funkcije?
b) Ali je v dobi računalnikov še smiselno študirati nivojske krivulje?
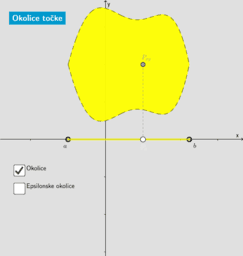
L9-L10 Razširimo pojem okolice. Na premici je interval, v ravnini je območje znotraj sklenjene krivulje, kaj pa v prostoru?
Kaj pa limita funkcije? Kaj pomeni trditev “ko točka teži k… , funkcija teži k…” ?
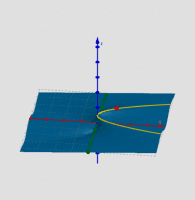
L11 Kaj pa odvod funkcije v prostoru? Obstaja povezava z odvodom funkcije v eni sami spremenljivki?
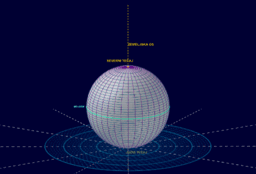
L12 -L13 Ali lahko "raztegnemo" kroglo na ravnino? Kako "neformalno" izračunamo površino krogle?
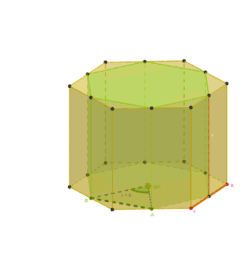
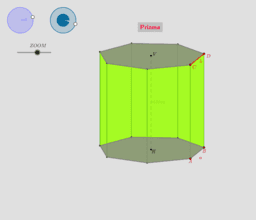
L14-L15-L16 Poglejmo od blizu naše stare znance: prizmo, stožec in valj
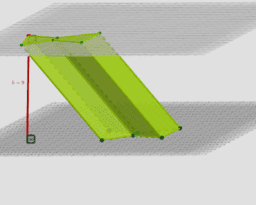
L17 V prejšnjih enotah smo videli, kako je npr. plašč valja mejna lega plašča prizme z nešteto mnogimi stranskimi ploskvami.
Ali lahko aproksimiramo plašč valja s pravokotniki, ali še bolje s trikotniki?
L18 In Pitagorov izrek?
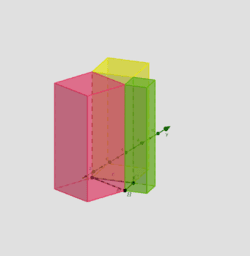
L19-L20 Ali obstaja kategorija teles, ki kljub različni obliki imajo isto prostornino? V pomoč nam pride Cavalierijevo pravilo!
L21 Limita zaporedja v krog včrtanih pravilnih mnogokotnikov je ploščina kroga. Kaj podobnega je tudi z limito prostornin v valj včrtanih prizm, in še več....
L21-L22 V prostoru so tudi take čudne ploskve, ki nimajo spodnjega in zgornjega dela in niti notranjosti in zunanjosti.
L23