Error en la Interpolación Polinomial
Error de interpolación
Supongamos que tenemos una serie de puntos con los cuales hemos construido el polinomio de interpolación que pasa a través de ellos y que además, contamos con la función original que genero dichos puntos. Entonces, el error de interpolación es la diferencia entre la función original y el polinomio de interpolación, evaluado en . Gráficamente es la distancia entre las gráficas de y evaluadas en alguna .
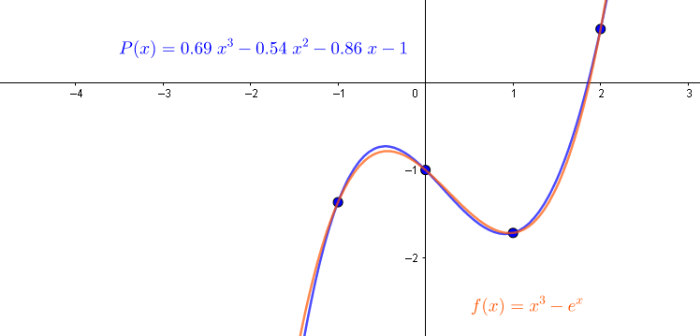
El teorema que veremos a continuación nos proporciona una formula que nos dará más información sobre el error de interpolación el cual a menudo se puede acotar a un límite de error.
Conocimientos Previos
Antes de enunciar y demostrar el Teorema para la Formula del Error en la Interpolación Polinomial es necesario un repaso con herramientas auxiliares que usaremos más adelante.
1. Teorema de Rolle. Sea una función continua en derivable en y tal que . Entonces existe un número en tal que .
2. Teorema generalizado de Rolle. Sea una función de clase ( representa a las funciones de clase continuas derivables veces) que se anula en algunos puntos del intervalo . Entonces existe un número en tal que .
3. Sobre las derivadas de ordenes mayores de un polinomio. Sea un polinomio de grado :
Entonces su -ésima derivada es constante:
,
y las siguientes derivas son cero:
.
Teorema (Formula del Error en la Interpolación Polinomial)
Sean parejas de puntos con distintas pertenecientes a un intervalo y sea . Denotemos por al polinomio de interpolación (de grado o menor) que ajusta dichos puntos. Entonces para cada existe un número tal que:
Demostración:
Si es algún la ecuación se vuelve cierta ya que ambos miembros se vuelven .
Para el caso donde utilizaremos la siguiente función auxiliar:
con
Observemos que y que se anula en puntos distintos . El Teorema generalizado de Rolle nos indica que existe un punto tal que . Calculando usando la proposición sobre las derivadas de polinomios tenemos:
se anula por el teorema sobre las derivadas de ordenes mayores de un polinomio
Al despejar obtenemos:
con lo que concluimos la demostración (Maximenko, s.f).
Observación
El Teorema afirma la existencia de un número con la propiedad escrita, pero no proporciona ningún procedimiento cómodo para calcularlo. En la práctica se calcula:
y se usa la siguiente cota superior del error: