Simplex Algorithmus MAX Programm
Grundlagen (Google Sheets - Video)
X Vorgabe der Strukturvariablen oder Nichtbasisvariablen x1,x2 . Die Basisvariablen x3 .. x7 werden im Start-Tableau als Schlupfvariablen eingetragen"
(ggf. ändern oder ergänzen).
Tablo, Gleichungssystem, beginnend mit den Nebenbedingungen f(x)<= b. Ungleichungen f(x) >= b ggf. "Umdrehen zu" (-1)f(x) <= -b , ergänzt durch die Basisvariablen xi (Schlupfvariablen) zu einer Gleichung. Zum Abschluss die Zielfunktion als Gleichung =0 (Eintrag der Zielfunktion im Tableau wird mit (-1) multipliziert!
Aus Tablo erzeuge ich das Ausgangstableau für den 1. Simplex-Schritt, Start (Zeile $5).
Ziel ist es durch Umformung der Start-Tableaus in der Zeile der Zielfunktion (Zeile n) ausschließlich positive Werte zu erzeugen.
9: A1:=Start Tableau A1 zuweisen
Einen Simplex-Schritt berechnen durch die Anwendung der Simplex-Schritt-Funktionen
| | Schritt-Berechnung | Schritt-Funktion | Anwendung auf A1 |
| 1: | Pivotspalte | PivotSpl | kleinster Koeffizient der Zielfunktion oder Eingabe Pivot-Spalte |
| 2: | Quotient b-Vektor | Qb (b/Ai Pivotspalte) | b-Spalte dividiert durch Koeffizienten der Pivotspalte |
| 3: | Pivotzeile | PivotZle | Zeile mit kleinstem Quotient aus Qb |
| 4: | Pivot-Zeilen-Element aus Ai | Pivot | Pivot = a(PivotZle, PivotSpl) dividiere Pivotzeile/ Pivot |
| 5: | Nächstes Tableau | A2 | addiere Pivot zu allen anderen Zeilen und erzeuge 0en in der Pivotspalte |
Zur JavaScript Umsetzung des Simplex-Algorithmus Zielfunktion als Gleichung =0 ans Ende der Liste stellen!
PivotSpl=1, PivotZle=2, Pivot {1, 0.4, 0.2, 0, 0.2, 0, 100}
copy A2 to A1
PivotSpl=3, PivotZle=1, Pivot {0, 1.26, 1, 0.19, (-0.11), 0, 92.59}
copy A1 to A1
SimplexAlgorithmusIntegerMAX
Beispiele
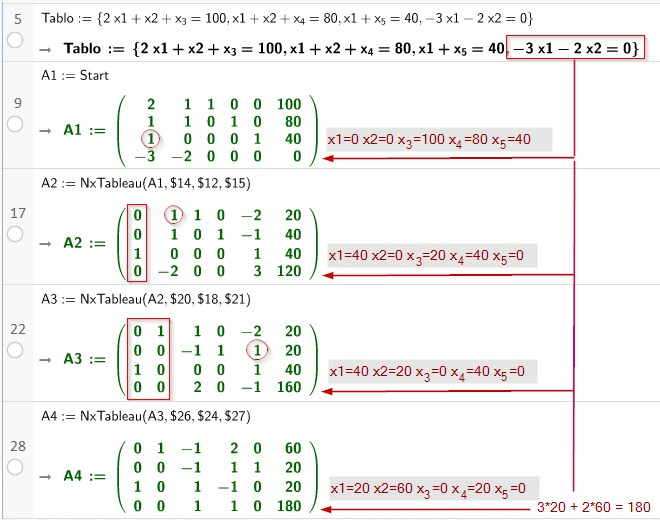
Im Schlusstableau ist der maximale Wert für die Zielfunktion in der B-Spalte (max=180) abzulesen.
Die x1=20 und x2=60 Werte stehen ebenfalls in der B-Spalte in den Zeilen, in denen die x1, x2 Koeffizienten durch die Umformungen verschoben wurden.
Beispiel entnommen https://sites.google.com/site/simplexverfahren/begriffe-von-a-bis-z
für ausführlichen Kommentierung des Algorithmus siehe dort.
maximize_lp(40*x1+20*x2,[
20*x1+7*x2<=1400, 7*x1+10*x2<=1600, 8*x1+2*x2<=500, x1<=50, x2<=150]
), nonegative_lp=true;
[556000/151,[x2=22200/151,x1=2800/151]]
Übung:
http://www.fernstudium-wiwi.de/simplextableau-umformung-fuer-dummies/
Tablo:={ 20*x1+7*x2+x_3=1400, 7*x1+10*x2+x_4=1600, 8*x1+2*x2+x_5=500, x1+x_6=50, x2+x_7=150, -40*x1-20*x2=0}
Tablo:={x1+x3+x_4=8, x1+x2+x_5=7, x1+2 x2+ x_6=12, -3*x1-2*x2-2 x3=0}
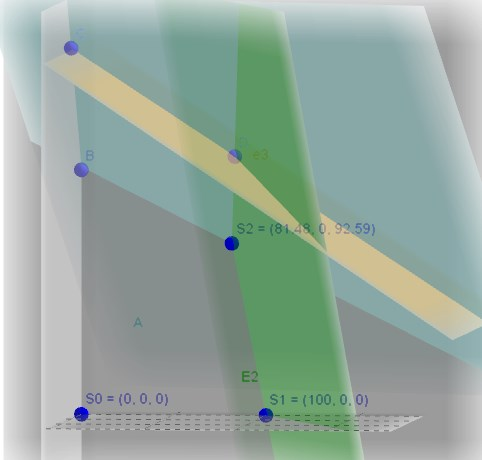
Lösungsraum mit den Ergebnissen der Simplex Tableaus
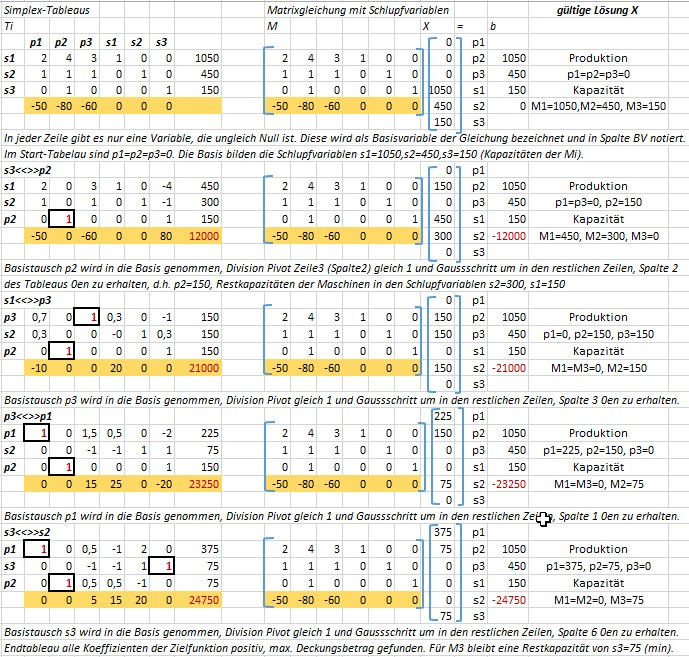
Beispiel mit TabCalc (MS Excel/Google Sheet
3 Produkte werden auf 3 Maschinen M1, M2 und M3 hergestellt. Die Belegungszeiten der Produkte auf der Maschine M1 betragen 2 Minuten für P1, 4 Minuten für P2 und 3 Minuten für P3; M1 besitzt eine freie Kapazität von 1.050 Minuten.
Alle Produkte belegen die Maschine M2 mit je einer Minute; die Kapazität dieser Maschine beträgt noch 450 Minuten.
Auf der dritten Maschine M3 kann nur P2 gefertigt werden; sie besitzt noch eine Kapazität von 150 Minuten. Die Belegungszeit von P2 auf M3 beträgt 1 Minute.
Der Deckungsbeitrag je Stück der 3 Produkte beträgt 50 € , 80 € bzw. 60 €.
a) Welche Stückzahlen sind jeweils herzustellen, damit der Gesamtdeckungsbeitrag maximal wird?
b) Wie groß ist der optimale Gesamtdeckungsbeitrag und wie hoch sind die freien Kapazitäten der drei Maschinen im Optimum?
Anwendung der Google Sheet
Grundlagen (Google Sheet - Video)
Grundlagen (Google Sheet - Video)
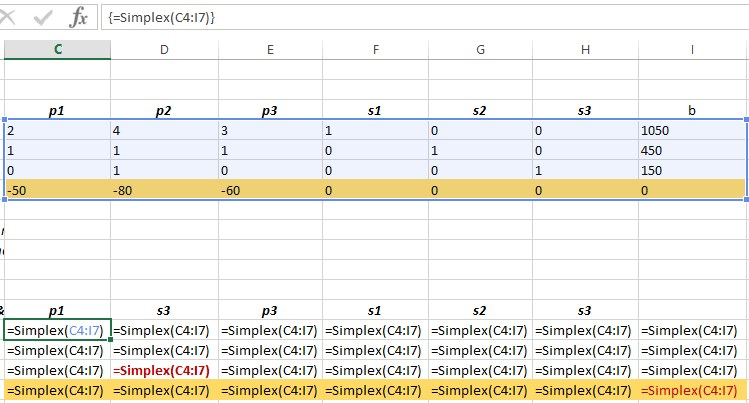
Tabellenkalkulation Simplex Code
Simplex Excel VBA Code enter an arbitrary answer to see code
Tabellenkalkulation Simplex Code
Simplex Javascript 4 Google Sheet enter an arbitrary answer to see code