Satelliti medicei
- Autore:
- Giulia Ortolani
INTRODUZIONE
I satelliti medicei furono osservati per la prima volta da Galileo il 7 gennaio 1610 grazie all'uso del cannocchiale. Egli vide infatti tre puntini luminosi e, inizialmente, credette fossero tre stelle vicino a Giove. In seguito, il 12 gennaio 1610 individuò una quarta stella e notò che le altre avevano mutato posizione. Continuò quindi le osservazioni e nelle notti seguenti si accorse che si muovevano sempre ad intervalli regolari e non si allontanano mai oltre un determinato limite dal pianeta. La loro posizione rispetto a Giove lo portò a pensare che fossero in orbita attorno al pianeta, conclusione a cui giunse già il 15 gennaio. Dopo essere riuscito a capire che orbitavano intorno a Giove, aggiunse questo argomento a quelli a sostegno della teoria eliocentrica copernicana: l’universo era policentrico e non tutti i corpi orbitavano intorno alla terra. Galileo chiamò i satelliti inizialmente Cosmica Sidera («stelle di Cosimo»), in onore del granduca Cosimo II dei Medici, e successivamente Medicea Sidera («stelle medicee»), in onore dell'intera casata dei Medici.
Galileo, nella conclusione del Sidereus Nuncius, parla così della sua scoperta:
“Abbiamo dunque un valido ed eccellente argomento per togliere ogni dubbio a coloro che, accettando tranquillamente nel sistema di Copernico la rivoluzione dei pianeti intorno al Sole, sono tanto turbati dal moto della sola Luna intorno alla Terra, mentre entrambi compiono ogni anno la loro rivoluzione attorno al Sole, da ritenere si debba rigettare come impossibile questa struttura dell'universo. Ora, infatti, non abbiamo un solo pianeta che gira intorno a un altro, mentre entrambi percorrono la grande orbita intorno al Sole, ma la sensata esperienza ci mostra quattro stelle erranti attorno a Giove, così come la Luna attorno alla Terra, mentre tutte insieme con Giove, con periodo di dodici anni si volgono in ampia orbita attorno al Sole.”
La Terra può trovarsi in prossimità del piano su cui giacciono le orbite dei satelliti medicei per alcuni mesi, ma ciò accade solo ogni sei anni circa. Tuttavia in questi periodi si può assistere anche a un centinaio di transiti dei satelliti davanti a Giove e di eclissi tra Giove e i satelliti o tra i satelliti stessi.
Grazie a questo fenomeno le ricerche furono facilitate. Diversi altri osservatori, tra cui Keplero, confermarono la scoperta e ne dedussero, come aveva fatto Galileo, che i nuovi astri ruotano attorno a Giove così come la Luna fa attorno alla Terra ed i pianeti attorno al Sole. I satelliti furono poi battezzati con i nomi di Io, Europa, Ganimede e Callisto, nomi di alcune amanti di Giove secondo la mitologia classica. Questi satelliti presentano una forma sferoidale e sarebbero considerati dei pianeti nani se orbitassero direttamente attorno al Sole.
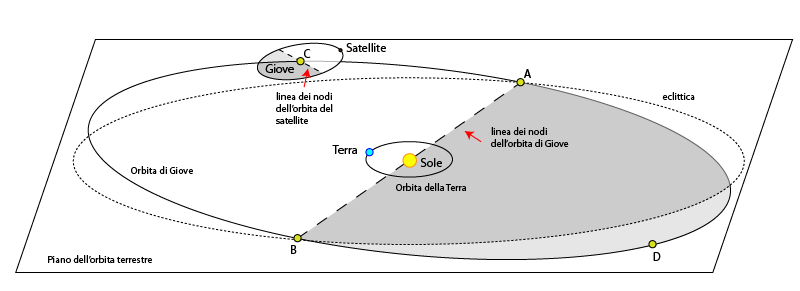
ROTAZIONE DI GIOVE ATTORNO AL SOLE
Giove ruota attorno al Sole seguendo un’orbita ellittica e, come tutti i pianeti, segue le leggi di Keplero. Prendendo come unità il raggio dell’orbita terrestre (1 Unità Astronomica, UA) l’orbita di Giove possiede un raggio di 5.2 UA. L’orbita di Giove intorno al Sole avviene lungo un piano che risulta inclinato di circa 1.3 gradi rispetto al piano dell’orbita terrestre: questo fatto comporta che circa metà dell’orbita di Giove avviene al di sopra di questo piano di riferimento (detto piano dell'eclittica) e l’altra metà al di sotto di esso. Nel diagramma in grigio è indicata la parte dell’orbita di Giove inferiore al piano dell’eclittica. La linea tratteggiata è la cosiddetta linea dei nodi dell’orbita di Giove, che rappresenta lo spartiacque tra posizioni di Giove al di sopra e al di sotto dell’eclittica: quando Giove si trova nei punti A o B della propria orbita, visto dalla Terra si troverà esattamente sull’eclittica e perciò avrà una latitudine eclittica esattamente pari a 0°. In corrispondenza del punto C Giove si vedrà dalla Terra a Nord dell’eclittica e perciò presenterà una latitudine positiva. Al contrario, nel punto D Giove avrà una latitudine eclittica negativa.
Anche i satelliti galileiani seguono orbite ellittiche, con parametri orbitali che rispettano le leggi di Keplero; tuttavia, considerata l’eccentricità molto vicina allo zero, si può parlare di orbite quasi circolari. Le loro inclinazioni orbitali sono molto piccole e non raggiungono il mezzo grado: in particolare, per Io, Europa, Ganimede e Callisto valgono rispettivamente 0.05°, 0.47°, 0.20° e 0.20°. A causa di questi valori molto bassi si può concludere che in media le orbite dei satelliti di Giove sono complanari rispetto all’equatore di Giove. Inoltre i satelliti, visti dalla Terra, si spostano avanti ed indietro da un lato all’altro di Giove seguendo un andamento sinusoidale, lungo un percorso in prima approssimazione rettilineo. Il primo ad accorgersi di questo fenomeno fu proprio Galileo.
ROTAZIONE INTORNO A GIOVE DEI QUATTRO SATELLITI MEDICEI
In questa animazione possiamo osservare un modello del moto dei satelliti medicei attorno a Giove.
https://ggbm.at/t7zDk3qw
VELOCITÀ DEI SATELLITI
Le velocità dei satelliti si possono ricavare dal secondo principio della dinamica:
in cui indichiamo con F la forza di attrazione gravitazionale e con a l'accelerazione centripeta. Esplicitando le forze nell'equazione precedente, si ha:
dove: F è la forza di gravità; R è la distanza del satellite dal centro di Giove; M è la massa di Giove (1,898 ∙ 1027 kg); m è la massa del satellite; G è la costante di gravitazione universale () e v è la velocità del satellite.
(1)
Da ciò si deduce che i satelliti più lontani dal pianeta hanno una velocità inferiore.Ed effettivamente è la conclusione a cui si arriva anche mettendo a confronto i dati sperimentali:
RISONANZA E PERIODO ORBITALE
Le orbite di Io, Europa e Ganimede sono legate tra loro da una risonanza orbitale, chiamata risonanza di Laplace, cioè i loro periodi orbitali stanno tra loro nel rapporto 1:2:4. Questo è dovuto alle forze mareali che si esercitano tra essi. Il periodo orbitale è il tempo che impiega un corpo orbitante per compiere un'orbita completa durante il suo moto di rivoluzione. La risonanza orbitale avviene quando due corpi orbitanti hanno periodi di rivoluzione tali che il loro rapporto è esprimibile in frazioni di numeri interi piccoli. Quindi i corpi esercitano una regolare influenza gravitazionale reciproca. Questo fenomeno può stabilizzare le orbite e proteggerle da perturbazioni gravitazionali.
Per ricavare la formula del periodo (T) si può partire da una relazione che vale nel moto circolare uniforme , da cui si ricava il periodo
Sostituendo v con la formula (1) si ottiene(2)
Quando le masse di entrambi i corpi orbitanti devono essere prese in considerazione, il periodo orbitale può essere calcolato con la formula
dove m1 e m2 sono le masse dei corpi considerati. Da questo si ricava che i satelliti più lontani impiegano un tempo maggiore per completare un’orbita intera
Il rapporto di risonanza orbitale tra Io, Europa e Ganimede è facilmente intuibile da questa animazione:
https://ggbm.at/qxtnXtkw
SINUSOIDE DEL MOTO DEI SATELLITI
Un diagramma di questo tipo riporta le posizioni relative a Giove dei quattro satelliti medicei. La rappresentazione consente di avere un'idea delle posizioni dei satelliti nel corso del tempo. La proiezione su un diametro delle posizioni di un punto materiale che si muove di moto circolare uniforme è un moto armonico. Se riportiamo in un diagramma cartesiano la posizione di un satellite in ordinata, col tempo in ascissa, avremo un diagramma orario che sarà una sinusoide. Ciascuna sinusoide sarà caratterizzata da un periodo (il periodo del satellite) da un'ampiezza (il semiasse maggiore dell'orbita, espresso in funzione del diametro di Giove) e da una fase (la posizione del satellite a un istante iniziale). Si tratta dunque di trovare quattro sinusoidi, di periodi, ampiezze e fasi diverse.
Per prima cosa occorre dunque porre i semiassi maggiori delle orbite in funzione del diametro di Giove (139.822 km):
Ottenuti questi valori, possiamo sostituirli nell'equazione generale del moto armonico:
Ottenute le equazioni della sinusoide si possono rappresentare i moti dei satelliti in funzione del tempo, così come mostrato nella seguente applet.
https://ggbm.at/K9fm3SUa
Giulia Ortolani