Construim Volums en tres dimensions
Anem a veure com podem construir diferents cossos geomètrics en tres dimensions per poder calcular-ne el volum i les àrees laterals.
Començarem construint un senzill cub.
Per això ens cal obrir la finestra 3D.
Un cop tenim el Geogebra obert, clicarem a Visualitza ---> Finestra gràfica 3D
Se'ns obrirà un uns eixos de 3 dimensions al costat dels típics eixos de coordenades.
Tancarem, de moment, la Finestra Gràfica de dos dimensions i la Finestra Algebraica (la de l'esquerra).
Així només tenim la finestra 3D. Podem fer que es vegin els eixos, una graella o el pla horitzontal, o podem fer que desapareguin, clicant als botons de sota el botó de la fletxa, 
.
Si no surt cap botó dels eixos o les graelles, clica a la fletxa petita que hi ha a sota de , i es desplegarà un petit menú com el següent:
.
Si no surt cap botó dels eixos o les graelles, clica a la fletxa petita que hi ha a sota de , i es desplegarà un petit menú com el següent:
Clica a sobre les diferents possibilitats per veure el que pots fer i deixar de fer. Clica a les diferents icones per descobrir les possibilitats.
Ara desplega el menú que hi ha a sobre de la piràmide, 
, i clica sobre el botó del cub, 
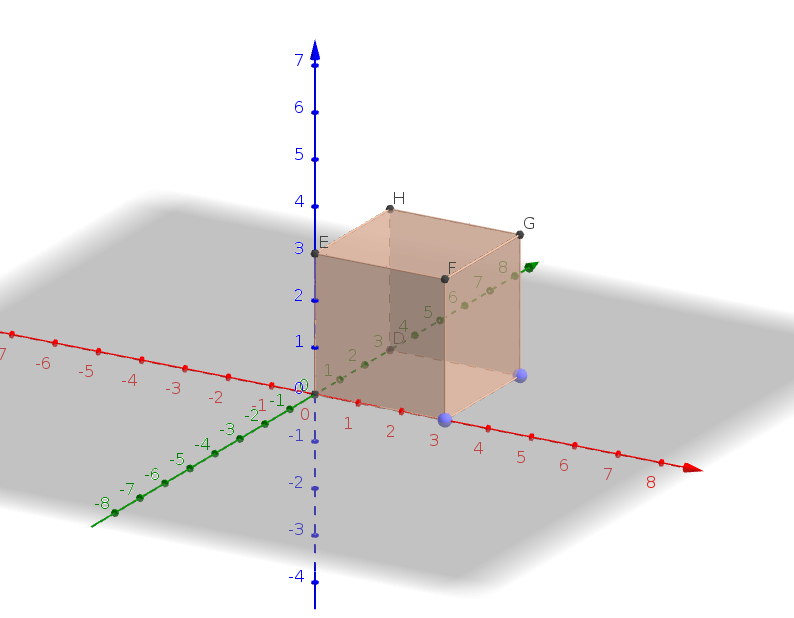
Ara, només et cal marcar dos punts, i el geogebra et generarà tot el cub a partir de l'aresta que hagis creat. Crea un cub de costat 3, i t'ha de quedar un objecte de l'estil següent:
, i clica sobre el botó del cub,
Ara, només et cal marcar dos punts, i el geogebra et generarà tot el cub a partir de l'aresta que hagis creat. Crea un cub de costat 3, i t'ha de quedar un objecte de l'estil següent:
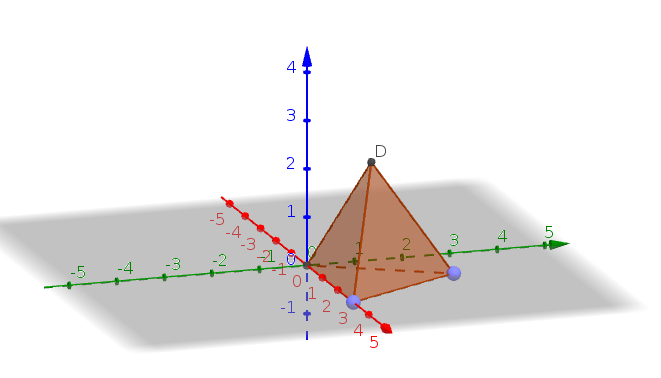
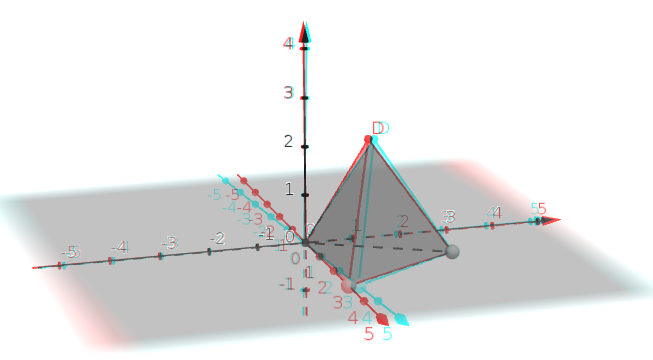
Ara fes el mateix amb el tetraedre, clicant a la figura següent: 
i marcant dos punts. En aquest cas, que l'aresta sigui de mida 3.
i marcant dos punts. En aquest cas, que l'aresta sigui de mida 3.
Un cop hagis fet això, prova de girar les vistes, mirant la planta, alçat i perfil. Canvia la perspectiva i fes que la figura que has creat vagi girant.
Prova ara, les ulleres 3D. Per fer-ho, cal clicar a la última icona del menú dels eixos i la graella de l'espai 3D i clicar a
Un cop clicat sobre les ulleres. El vostre espai 3D es veurà ara amb tons vermells i blaus. Per això les ulleres tenen aquests dos colors. Si ara moveu la figura al llarg de la pantalla, veureu que la sensació és que la figura surt de la pantalla.
Ara ja podem crear també piràmides i prismes a partir de figures planes.
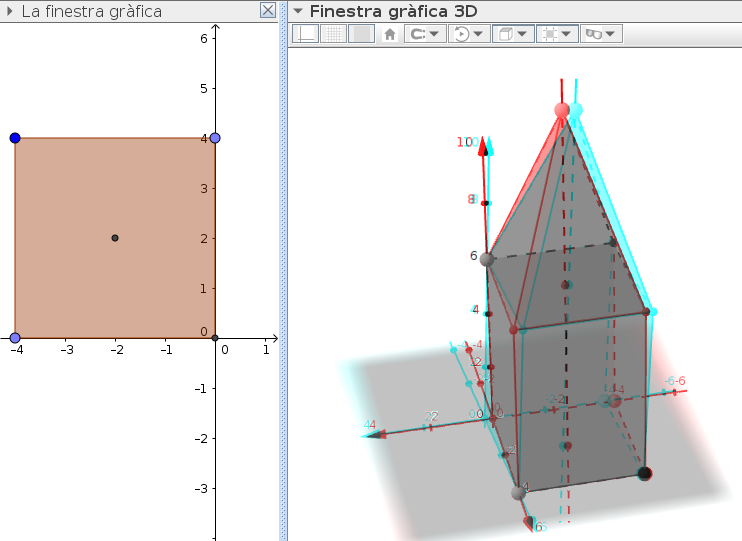
Torna a obrir la Finestra gràfica, i dibuixa-hi un quadrat. Sorpresa!
També es veu al 3D. Esborra el quadrat i, per exemple, dibuixarem un pentàgon regular, l'estirarem i en farem un prisma de base rectangular.
Primer de tot, volem tornar a veure la Finestra Gràfica. Clica a Visualitza --> La Finestra Gràfica.
Ara desplega el menú d'on hi ha 
i busca el Polígon Regular 
. Abans de tornar a clicar-hi, posa el ratolí a sobre i et dirà les condicions per fer servir l'eina.
Això és important, si no saps com va una eina, només posa el ratolí a sobre de l'eina i et sortirà una petita ajuda explicant el que fa l'eina. En aquest cas, per exemple, si ens posem a sobre de Polígon Regular, obtenim la següent:
i busca el Polígon Regular . Abans de tornar a clicar-hi, posa el ratolí a sobre i et dirà les condicions per fer servir l'eina.
Això és important, si no saps com va una eina, només posa el ratolí a sobre de l'eina i et sortirà una petita ajuda explicant el que fa l'eina. En aquest cas, per exemple, si ens posem a sobre de Polígon Regular, obtenim la següent:
En aquest cas, ens recomana que seleccionem dos punts, que serà una aresta, a partir de la qual generarà tot el polígon. Un cop marcats els dos vèrtexs d'un costat, cal que li diem de quan costats volem fer el polígon. En aquest cas, li direm 5.
Vés en compte, que si cliques sobre la finestra 3D o sobre la finestra gràfica, la barra de les eines canvien, no són les mateixes.
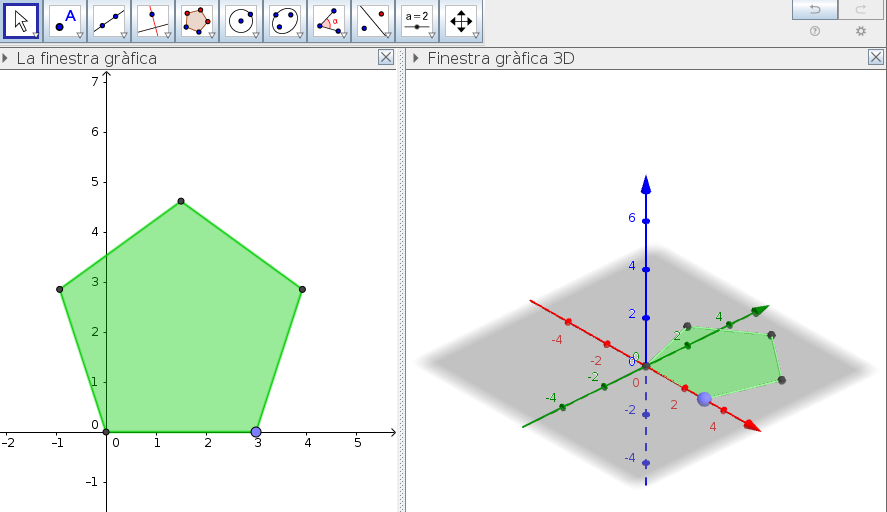
Ara, crearem un prisma de base pentagonal.
Per fer-ho, clicarem a la finestra 3D, i desplegarem les eines que hi ha a i cliquem a sobre de l'eina Prisma: 
. Si ens posem a sobre, veiem que l'ajuda ens diu que hem de crear la base del prisma marcant nosaltres tots els punts o podem clicar directament sobre el polígon que ja tenim creat. En aquest cas, clicarem a sobre el pentàgon per marcar quina és la base, i després mourem el ratolí per estirar el prisma. En aquest cas, el farem recte i podem clicar a sobre d'algun punt de l'eix vertical de color blau.
Un cop el tenim fet, podem canviar el color i l'opacitat de l'objecte si editem les propietats.
Però en aquest cas, tornem a clicar a les ulleres 3D per veure el prisma tridimensional.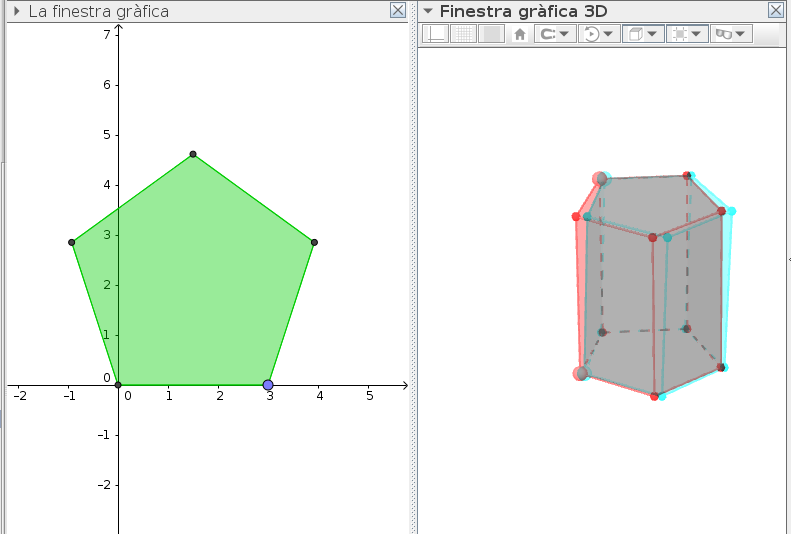
Ara veurem una altra propietat molt important del Geogebra. Que ens calcula el valor de les arestes, les àrees i el volum de les figures.
Per veure-ho, obrirem la Finestra Algebraica. Cliquem a Visualitza ---> Finestra Algebraica.
En aquí tenim totes les dades del Prisma que hem creat.
El geogebra separa segons tipus d'objecte. En aquest cas tenim
- Els punts (que venen donats amb dues o tres coordenades segons a on els hem creat)
- Els Segments (el qual ens està donant les seves mides) en unitats de longitud (cm o m). Li ha posat nom d'arestes indicant origen i final.
- Quadrilàters (Que es refereix a les cares rectangulars laterals del prisma). Del qual ens dóna el valors de l'àrea, en aquest cas unitats d'àrea (cm2 o m2).
- Polígon (que hem creat a la Finestra gràfica 2D), el qual ens dóna el valor de l'àrea.
- Pentàgon (que s'ha creat al fer el prisma, és la cara de dalt), també ens dóna l'àrea.
- Prisma, del qual ens dóna el valor del Volum.
Un cop has après a fer-ho, ara toca calcular volums i àrees.
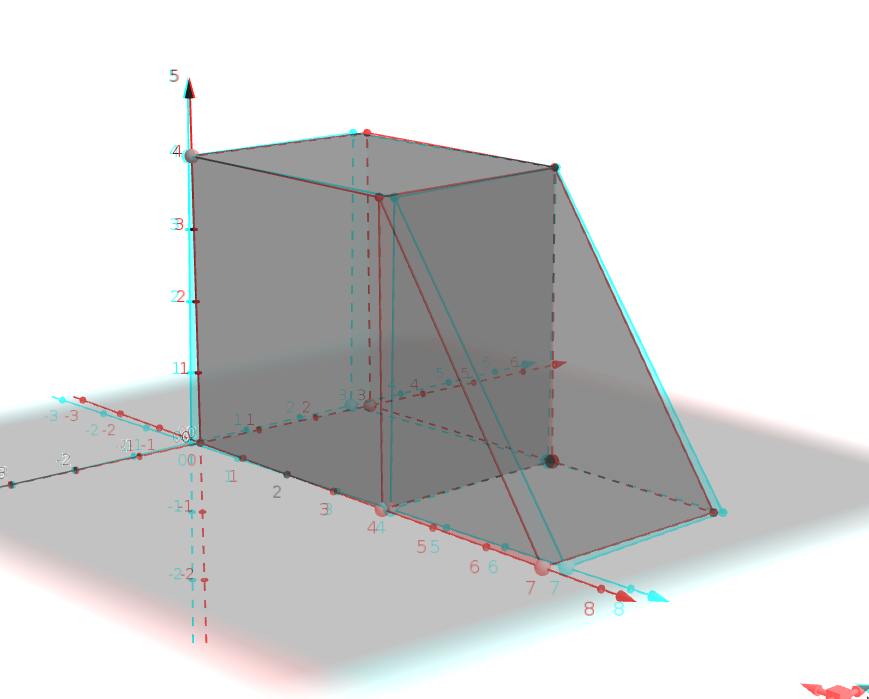
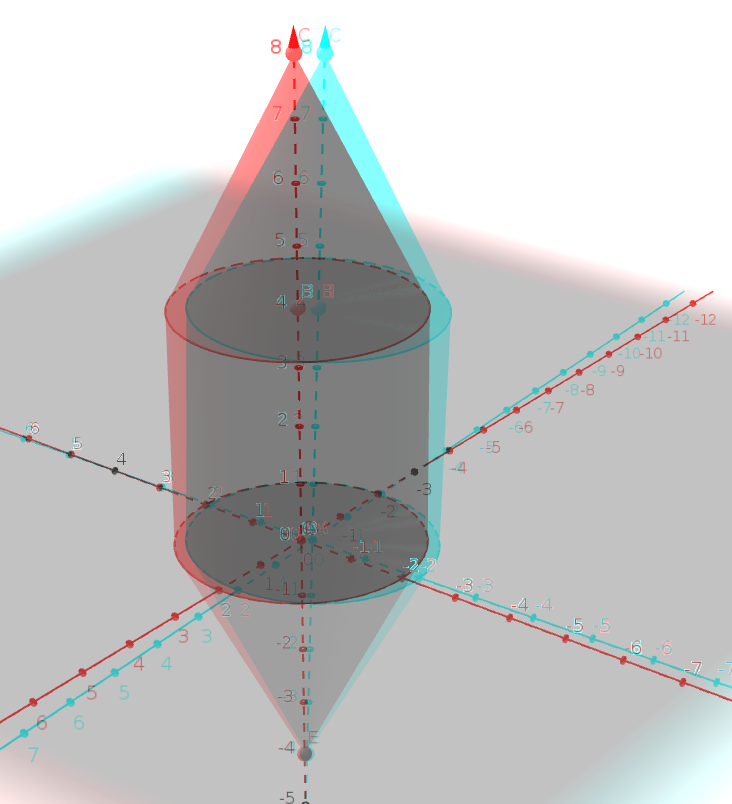
Construeix amb el Geogebra les dues següents figures i calcula'n la seva àrea lateral i volum. Fixa't amb les mesures. En el de la caseta, per poder crear la punta de la teulada, hem buscat el punt mig de la cara de dalt i de baix, hem dibuixat la recta que els uneix i hem construït la piràmide a través de la recta.
