Mit Vektoren einfach rechnen
Was sind Vektoren?
Ein Vektor ist eine Linie im drei dimensionalen Raum, welche eine bestimmte Länge (Betrag hat). Vektoren werden immer mit einem Strich über dem jeweiligen Buchstaben dargestellt. Hier sind Vektoren Fettgedruckt (z.B. a)! Hingegen sind Punkte einfach nur Punkte im Raum und keine Vektoren. Ein Punkt ist einfach nur im Raum und ein Vektor gibt eine Richtung im Raum an.
Punkte im Koordinatensystem
Um einen Punkt in einem Koordinatensystem im dreidimensionalen Raum einzeichnen zu können, brauchen wir erst einmal die Koordinaten des Punktes. Dabei bestehen solche Koordinaten aus einer x1-,x3- und x3 Koordinate (oder auch x-,y-,z Koordinate). Die korrekte Schreibweise wäre dann Punkt A (x1/x2/x3) oder auch A (x/y/z)Am einfachsten Zeichnet man solche Punkte ein, mittels Wegbeschreibung: Man geht x Schritte der x1- oder x-Achse entlang, dann x Schritte nach links oder Rechts (x2- bzw. y-Achse) und dann x Schritte hoch oder runter (x3- bzw. z-Achse). Punkte und Vektoren können auch mit folgender Schreibweise dargestellt werden:
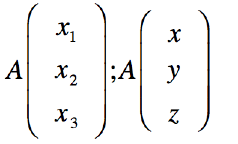
Vom Ursprung aus kann man dann einen Vektor bilden, welcher die Richtung angibt in welche Richtung wir "gehen" müssen um beim Punkt A anzukommen. Dieser Vektor wird auch Stützvektor genannt (in der Graphik Vektor a). Wenn wir von Punkt A zu Punkt B wollen, müssen wir angeben in welche Richtung wir wollen. Somit bilden wir den Richtungsvektor b. Diesen Vektor berechnet man, in dem man den Punkt B vom Punkt A abzieht.
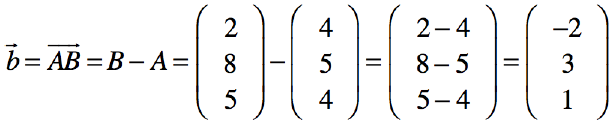
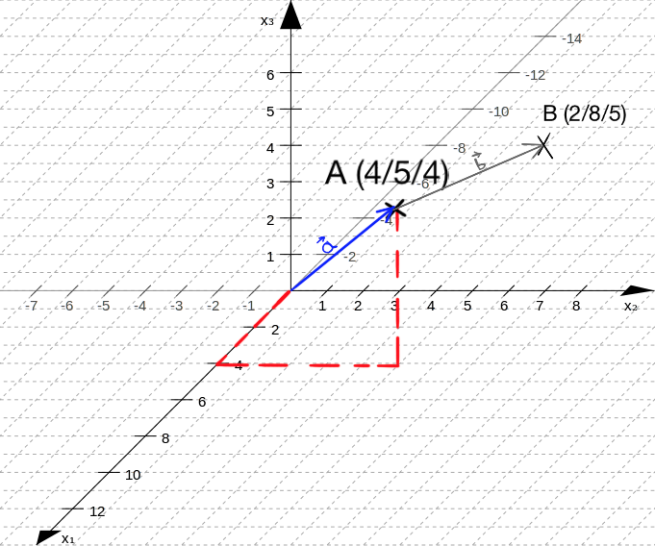
Betrag eines Vektors
Ein Vektor hat immer eine bestimmte Länge. Also können wir theoretisch ausrechnen, was wie eine Strecke wir laufen müssen, wenn wir von Punkt A nach B laufen bzw. entlang des Vektors b laufen. Hier für rechnet man mithilfe des Satz von Pythagoras die Länge des Vektors aus. Die Striche links und rechts neben dem Vektor nennt man Betragsstriche! Wenn wir einen Betrag ausrechnen, dann haben wir keine cm oder m, sondern Längeneinheiten (LE). Solange die Aufgabe nicht angibt, in welchen Einheiten gerechnet wird, schreiben wir immer in Längeneinheiten!
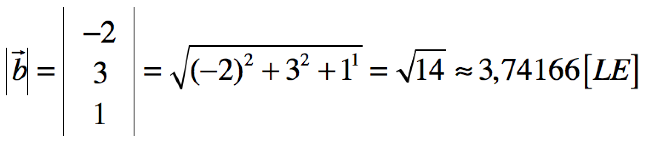
Aufgaben
A (Akjsdbasjdn)
asdasdasd
asdadasda