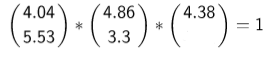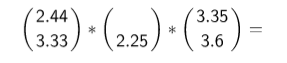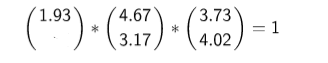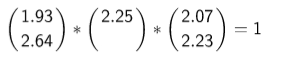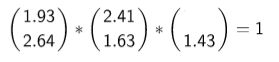Teorema de CEVA
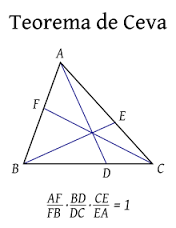
El teorema de Ceva es un teorema de geometría elemental. El teorema establece que dado un triángulo ABC, y los puntos D, E, y F que se encuentran sobre los lados BC, CA, y AB respectivamente, los segmentos AD, BE y CF son concurrentes si y solo si
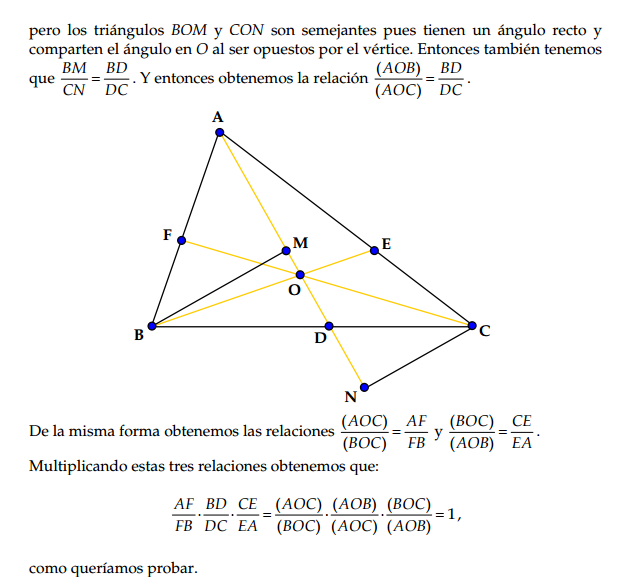
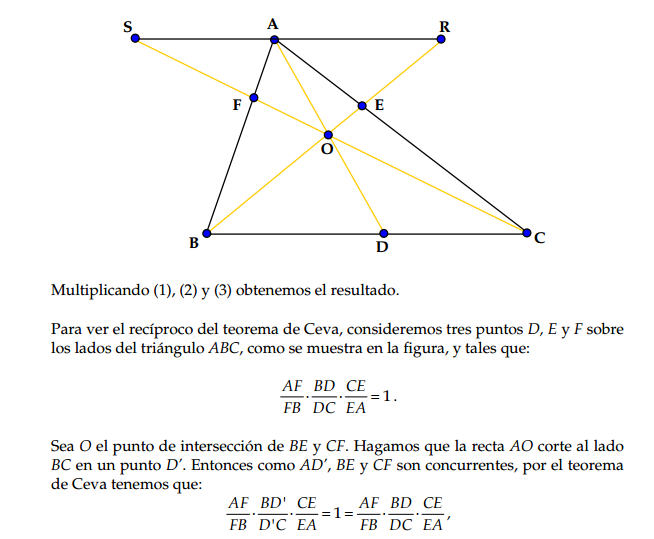
Demostración



¡Ahora velo tu mismo!
Mueve los vértices del Triángulo y comprueba que se cumple para todos los casos
Ejercicios
Puedes ayudarte con el Applet, encuentra el valor que falta en los siguientes casos: