Integral Dupla
Integral Dupla
A integral dupla de uma função de duas variáveis representa o volume entre o gráfico e o plano que contém seu domínio.Segundo Anton (2014, p.1039, V.II) “[...] uma integral dupla de uma função f(x,y) é definida em uma região fechada finita R do plano xy.[...]”
Superfície de Integração e Região de Integração
Região de integração
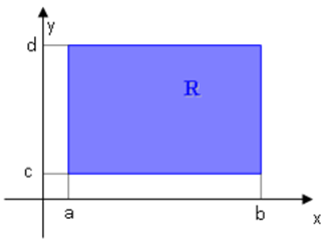
Volume entre a região e a superfície
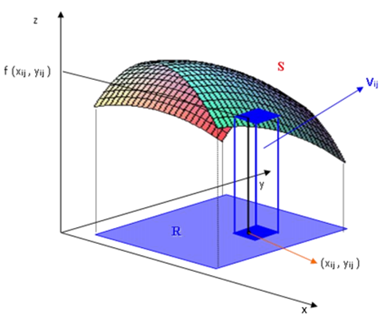
Volume por construção de prismas

Questões:
Integral dupla 1
Integral dupla 2
Integral dupla 3
5) (Gonçalves,2007, p.242) , onde R éa região delimitada por e
6) (Gonçalves,2007, p.242) , onde R éa região delimitada por , e .
7) (Gonçalves,2007, p.243) , onde R éa região delimitada por , e .
Integral dupla 7
9) (Gonçalves,2007, p.243) , onde R éa região delimitada por , , e .
10) (Gonçalves, 2007, p.243) , onde R éa região delimitada por , e .
Questões de Área com Integral Dupla:
1) (Gonçalves,2007, p.263) Calcular a área da região R delimitada por e .
2) (Gonçalves,2007, p.271) Calcular a área da região R delimitada por , e .
3) (Gonçalves,2007, p.271) Calcular a área da elipse .
4) (Gonçalves,2007, p.271) Calcular a área da região delimitada por , e .
Integral Dupla Área 4
Integral Dupla Área 5
Questões de Volume com Integral Dupla:
1) (Gonçalves,2007, p.256) Calcule o volume do sólido acima do plano delimitado por .
2) (Gonçalves,2007, p.258) Calcule o volume do sólido abaixo do plano delimitado por .
3) (Gonçalves,2007, p.259) Calcule o volume do sólido de limitado por e .
4) (Gonçalves,2007, p.261) Calcule o volume do sólido no primeiro octante, delimitado pelos cilindros e .
Integral Dupla Volume 4
Integral Dupla Volume 5 a
b) , , ,, e .
c) , , e .
d) , , .
e) , e .
f) , , , , e
g) , e .
Integral Dupla Volume 5 g
4) (Gonçalves,2007, p.261) Calcule o volume do sólido no primeiro octante, delimitado pelos cilindros e .