Das Verhalten im Unendlichen
Als nächstes untersuchen wir, wie sich der Graph im Unendlichen, d.h. ganz auf der rechten Seite () bzw. ganz auf der linken Seite () verhält. Kurz spricht man deshalb vom Verhalten für . Unsere Frage lautet: Wie kann man anhand des Funktionsterms herausbekommen, wie sich der Graph am rechten und linken Rand verhält?
Wir betrachten dazu, wie sich eine ganzrationale Funktion verhält, wenn der Betrag von x immer größer wird. Im folgenden Applet ist eine ganzrationale Funktion gegeben. Mit Hilfe des Schiebereglers kann man den x-Wert sehr groß positiv bzw. sehr groß negativ werden lassen. Tun Sie dies. Welcher Term entscheidet bei unendlich großen Beträgen von x über das Vorzeichen von dem Gesamtergebnis?
Als Ergebnis halten wir fest: Das Verhalten für unendlich große x-Werte wird von dem Summanden mit dem größten Exponenten dominiert. Deshalb können wir uns bei diesem Punkt der Untersuchung allein auf diesen Term konzentrieren.
Im obigen Beispiel sorgt also der erste Term dafür, dass für große positive x die Funktionswerte positiv unendlich werden. Und für große negative x sorgt der Term dafür, dass die Funktionswerte negativ unendlich werden.
Für den Graphen bedeutet dies: Auf der rechten Seite geht er nach oben, und auf der linken Seite geht er nach unten.
Kurz bringt man diesen Gedanken folgendermaßen auf den Punkt:
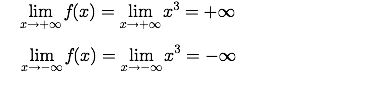
Und noch kürzer so:
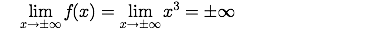
Betrachten wir abschließend das Beispiel der Funktion . Es gilt:
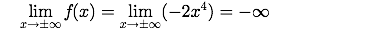
Das heißt, dass der Graph von f auf der linken und auf der rechten Seite jeweils nach , d.h. nach unten geht. Dies zeigt die folgende Abbildung.

Abschließende Aufgabe
Bestimmen Sie das Verhalten im Unendlichen der beiden Funktionen und Kreuzen Sie richtig an und überprüfen Sie Ihre Lösung, indem Sie auf den Button "Überprüfen" klicken.