Test jezelf
Vraag 1
Bekijk de grafiek van f(x) = - x3+12x.
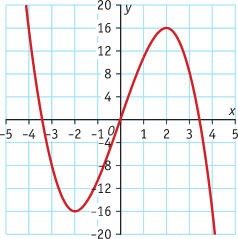
a. Welke soorten daling en stijging zie je in de grafiek? Geef de bijbehorende intervallen.
b. Geef de extreme waarden van de grafiek.
c. Voor welke waarde van x is de snelheid van stijgen het grootst?
Vraag 2
Gegeven is een functie met voorschrift f(x) = 18x−x3 . Plot de grafiek.
a. Geef aan op welke intervallen de grafiek dalend dan wel stijgend is en om welk soort stijging of daling het daarbij gaat. Rond indien nodig af op twee decimalen.
b. Geef aan welke extreme waarden er zijn, in twee decimalen nauwkeurig.
c. Geef aan voor welke waarde van x de snelheid van stijgen het grootst is.
Vraag 3
Bekijk de grafiek die hoort bij een parachutesprong vanaf 3500 meter hoogte. Eerst maakt de parachutist een vrije val en daarna opent hij zijn parachute.
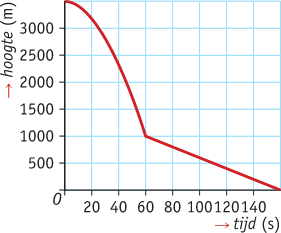
a. Na hoeveel seconden heeft hij zijn valscherm geopend?
b. Hoe zie je dat aan de grafiek?
c. In de periode van vrije val is de grafiek toenemend dalend. Wat betekent dit voor de valsnelheid?
d. Als de parachute open is, is de valsnelheid constant. Hoe zie je dat aan de grafiek?
e. Hoe groot is de valsnelheid als de parachute open is?
Vraag 4
Gegeven is de functie f met voorschrift f(x) = 0,5x4−4x2+8.
a. Welke extremen heeft deze functie?
b. Op hoeveel intervallen is bij de grafiek van f sprake van toenemende daling?
Vraag 5
Sofie rijdt met de auto naar de supermarkt. De eerste 7 seconden trekt ze eerst rustig maar daarna snel op, daarna rijdt ze 15 seconden met een constante snelheid om vervolgens 10 seconden lang geleidelijk af te remmen, totdat ze stil staat voor een verkeerslicht. Ze staat daar 30 seconden stil. Als het groen is, trekt Sofie geleidelijk op en na 8 seconden rijdt ze weer met een constante snelheid, totdat ze na 2 minuut bij de supermarkt is aangekomen en in 12 seconden geleidelijk afremt totdat ze stil staat.
Beschrijf met intervallen de soorten stijging en daling van de snelheid die je in deze situatie hebt.