Kopie van Minder brave transformaties
1. Brave Gelijkvormigheden
In de meetkunde komen een aantal heel brave transformaties voor: ze bewaren vorm en grootte.
Spiegeling, verschuiving en draaiing – en meer algemeen elke verplaatsing of omkering – zijn
isometriën.
Gelijkvormigheden zorgen ervoor dat een figuur en zijn beeldfiguur gelijkvormig zijn.
Een isometrië is dus een bijzondere gelijkvormigheid.
Een homothetie is een typische gelijkvormigheid:
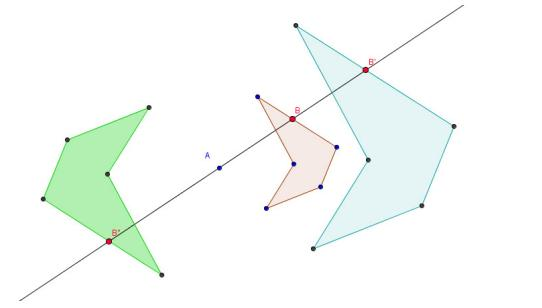
voorbeelden:
- de homothetie met centrum A en factor 2 beeldt de roze figuur af op de blauwe.
- de homothetie met centrum A en factor - beeldt de roze figuur af op de groene
Ook al is een homothetie wat avontuurlijker dan bijvoorbeeld een spiegeling, toch lijkt ze nog in niets op(wiskundige) transformaties die gebruikt worden in animatietechnieken zoals
morphing.

Ook in het werk van Escher duiken vervormende transformaties op met verrassende effecten:
De vogels links worden in een aantal stappen getransformeerd tot...

Animatiefilm op basis van een werk van Escher
Vervormende transformaties in GeoGebra
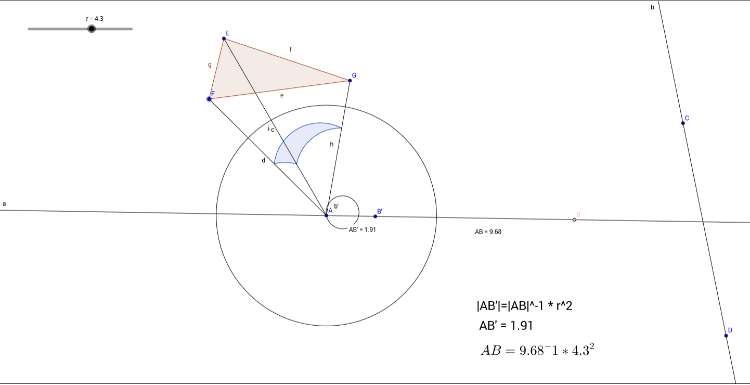
Onderzoek de "cirkelinversie" in Geogebra.
Wat is de definitie?
|AB'|=|AB|^-1 * r^2
Welke eigenschappen kan je ontdekken?
Als je de straal op nul zet of je punt samenvalt met het middelpunt van de cirkel zal je geen beeld vinden.
Cirkelinversie van een rechte:
*Dit levert een kleinere cirkel op.
*Hoe dichter de rechte bij cirkel komt, hoe groter de andere cirkel wordt.
*Wanneer de rechte door het middelpunt gaat, bestaat er geen beeld.
Cirkelinversie van een cirkel:
Vervormende transformaties in GeoGebra
Onderzoek de "cirkelinversie" in Geogebra.
Wat is de definitie?
|AB'|=|AB|^-1 * r^2
Welke eigenschappen kan je ontdekken?
Als je de straal op nul zet of je punt samenvalt met het middelpunt van de cirkel zal je geen beeld vinden.
Cirkelinversie van een rechte:
*Dit levert een kleinere cirkel op.
*Hoe dichter de rechte bij cirkel komt, hoe groter de andere cirkel wordt.
*Wanneer de rechte door het middelpunt gaat, bestaat er geen beeld.
Cirkelinversie van een cirkel:
*snijden de rechten elkaar krijg je een rechte die de snijpunten verbind.
*Raken de cirkels elkaar krijg je een cirkel die door dat raakpunt gaan.
*Anders krijg je een cirkel.
Inversie van een punt