Distancias: punto, recta y plano
Distancia entre un punto y un plano
Corresponde a la menor distancia entre el plano () y el punto (Q). Esto corresponde a la perpedicular trazada desde el punto hasta el plano.
Para esto:
- Se toma un punto del plano (P).
- Se crea un vector entre los puntos (P y Q).
- Se calcula la proyección del vector PQ en el vector normal del plano

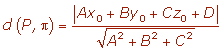
Ejemplo
Encontrar la distancia entre el punto Q=(1,5,-4) y el plano a: 3x-y+2z = 6.
Ejercicio: Distancia entre planos paralelos
Imaginemos que ahora tienes dos planos paralelos en R3 y necesitas obtener la distancia entre ellos, por ejemplo:
y
Solución
- Intenta obtener un punto que pertenezca al plano.
- Obtenga la distancia del punto al plano
Distancia entre un punto y una recta
La forma más sencilla de obtener la distancia entre un punto y una recta en el espacio, es mediante la fórmula:
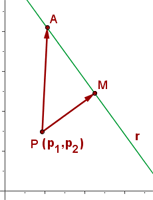
Como podemos ver, será necesario encontrar un punto que satisfaga la ecuación A. Luego, necesitaremos un vector desde el punto de la recta al punto inicial (AP). La distancia corresponde a la menor distancia del punto a la recta r, mediante la ecuación:
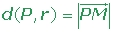
Siendo Ur el vector dirección de la recta.
Ejemplo
Encontrar la distancia entre el punto P = (1,3,-2) y la recta