Grafický součet úhlů
Zadání příkladu
Za využití předcházející úlohy graficky sečtěte úhly = 20° a = 125°
Applet
Postup vytvoření appletu
Jak už se v zadání píše, využíváme předchozí úlohu. Úhly alfa a beta si tedy sestrojíme podle předchozího postupu a v této části se budeme věnovat jen samotné konstrukci součtu. V postupu se často objeví, že kružnici nahradíme obloukem, to znamená, že na vytvořené kružnici sestrojíme oblouk a poté kružnici skryjeme. Toto děláme pro přehlednost, stejně tak při rýsování na papír většinou kružnice neděláme celé, ale pouhé obloučky. Stejně tak mnohdy v GeoGebře nahradíme přímku či polopřímku úsečkou. Stejně tak, jako v prvním bodě.
| 1. |  | sestrojíme úsečku, skryjeme jeden krajní bod, druhý bude vrcholem |
| 2. | 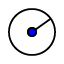 | sestrojíme kružnice o stejném poloměru (například 2) u všech tří vrcholů |
| 3. | 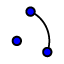 | kružnice nahradíme oblouky, skryjeme krajní body |
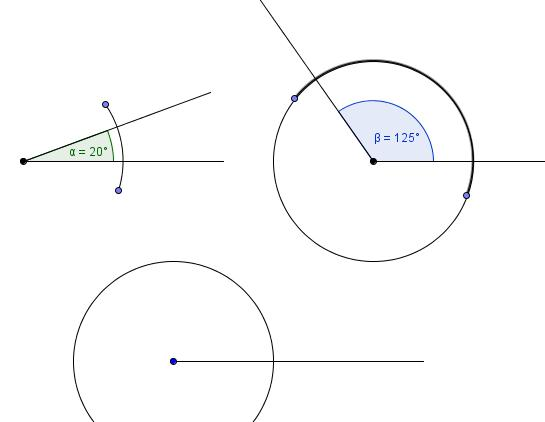
| 4. |  | vytvoříme průsečíky oblouků s rameny úhlů |
| 5. | 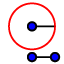 | poloměr: vzdálenost průsečíků ramen s obloukem u úhlu střed: průsečík oblouku s ramenem u nově tvořeného úhlu |
| 6. |  | právě vzniklou kružnici nahradíme obloukem a kružnici skryjeme |
| 7. |  | průsečík oblouků u nově tvořeného úhlu |
| 8. |  | polopřímka z vrcholu procházející průsečíkem z kroku 7 |
| 9. |  | polopřímku nahradíme úsečkou, skryjeme krajní bod |
| 10. |  | poloměr: vzdálenost průsečíků ramen s obloukem u úhlu střed: průsečík oblouků vzniklý v kroku 7 |
| 11. |  | právě vzniklou kružnici nahradíme obloukem a kružnici skryjeme |
| 12. |  | vytvoříme průsečík tohoto oblouku s obloukem u vrcholu nově tvořeného úhlu |
| 13. |  | polopřímka z vrcholu procházející průsečíkem z předchozího kroku |
| 14. |  | polopřímku nahradíme úsečkou, skryjeme krajní bod |
| 15. |  | pomocí bodů na oblouku zobrazíme hodnotu přeneseného úhlu |
| 16. |  | pomocí bodů na oblouku zobrazíme hodnotu přeneseného úhlu |
| 17. |  | pomocí bodů na oblouku zobrazíme úhel vytvoříme popisek |