Esquema
Jane Albre dünaamilised slaidid 12. klassile
Jane Albre-Anderseni koostatud dünaamilised slaidid 12. klassile.
Käesolev õppematerjal on valminud Tiigrihüppe Sihtasutuse toel. Õppematerjali autor on Jane Albre-Andersen. Õppematerjali seadis GeoGebra raamatuks Sirje Pihlap.
Alljärgnevalt on toodud kommentaarid õpetajatele koostatud kõigi 60 dünaamilise slaidi kasutamise kohta. Slaidid jagunevad nelja suuremasse kategooriasse: integraal, sirged ja tasandid ruumis, tasandigeomeetria kordamine ja hulktahukad ja pöördkehad. Osad slaidid on koostatud 12. klassi matemaatikaõpiku (L. Lepmann, T. Lepmann, K. Vels-ker, Koolibri, 2003) jooniste ja ülesannete lahenduskäikude dünaamiliseks visualiseerimiseks. Ülesannete korral on tekst reeglina lisatud slaidi ette.
Slaidide ja animatsioonide ülesehituses on püütud järgida koolis kasutatavat ülesannete lahendamise käiku. Näiteks ülesande korral, kus tuleb leida funktsiooni graafiku ja x teljega piiratud kõvertrapetsi pindala, antakse lahenduskäik järgmiselt:
1. esitatakse funktsioon algebralisel kujul;
2. antakse funktsiooni graafiku lõikepunktid x-teljega;
3. joonestatakse funktsiooni graafik;
4. värvitakse kõvertrapets, mille pindala otsitakse;
5. kirjutatakse välja integraal, mida on vaja leida;
6. antakse vastus.
Antud slaidide kasutamisel on olulised ka õpetaja sõnalised kommentaarid ja selgitused slaididel toimuva kohta, sest õpilased omandavad materjali paremini, kui saavad infot samaaegselt nii verbaalselt kui visuaalselt.
Dünaamilistel slaididel saab õpetaja ise teatud määral kujundust muuta. Õpetajal on võimalik tähistusi, teksti ja joonist slaidil hiirega nihutada. Lisaks on mõningatel slaididel võimalus liuguri abil teljestiku pööramiseks. Selle juures on oluline jälgida, et õpilasele tähtis info ei jääks varju.
Reeglina tähistavad sinised punktid slaididel punkte, mida on võimalik hiirega liigutada. Siniste punktide liigutamisel on võimalik jälgida nendest sõltuvate objektide muutumist slaidil.
Kõikide slaidide üleval paremas nurgas asub slaidi lähtestamise nupp, millele vajutades taastatakse slaidi algkuju. See on oluline just siis, kui slaidil on vabasid objekte palju nihutatud ja tekib vajadus kiiresti saada tagasi slaidi algkuju.
Mitmetel slaididel asuvad märkeruudud, millele klõpsates on võimalik ekraanile tuua vihjeid või vastuseid eelnevalt esitatud küsimustele.
Animeeritavatel slaididel asub ekraani allääres navigeerimisriba, mille abil on võimalik õpetajal näidata järgmist või eelmist animatsioonietappi, minna animatsiooni algusesse või lõppu. Teine võimalus on animatsiooni taasesitamise kiiruse valimine. Sel juhul esitatakse animatsiooni etapid õpetaja poolt määratud ajavahemiku järel pärast nupule vajutamist.
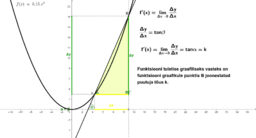
Tabla de contenidos
Integraal
- Tuletise geomeetriline vaste
- Funktsiooni algfunktsioonid
- Etteantud punkti läbiv algfunktsioon
- Pindalade ligikaudne arvutamine
- Kõvertrapetsi pindala lõigul
- Kõvertrapetsi pindala sõltuvus argumendist x
- Funktsioonide f(x) ja S(x) omavaheline seos
- Astmefunktsiooni graafik
- Määratud integraal piirväärtusena
- Pindala arvutamine. Ülesanne 81
- Pindala arvutamine. Ülesanne 82
- Pindala arvutamine. Ülesanne 83
- Pindala arvutamine. Ülesanne 84
- Pindala arvutamine. Ülesanne 85
- Pindala arvutamine. Ülesanne 87
- Pindala arvutamine. Ülesanne 89
- Pindala arvutamine. Ülesanne 91
- Pindala arvutamine. Ülesanne 92
Tasandigeomeetria
Sirged ja tasandid ruumis
- Punkti asukoht ruumi esimeses oktandis
- Koordinaatteljestik ruumis
- Ruumi kaheksa oktanti
- Punkti koordinaadid ruumis
- Punkti asukoha kujutamine ruumis
- Kahe punkti vaheline kaugus ruumis
- Paralleelsed sirged
- Kiivsirged
- Kahe lõikuva sirge vaheline nurk
- Kiivsirgete vaheline nurk
- Sirge ja tasandi vastastikused asendid
- Sirge ja tasandi paralleelsuse tunnus
- Punkti projektsioon tasandil
- Tasandiga paralleelse sirge kaugus tasandist
- Lõigu projektsioon tasandil
- Sirge ja tasandi vaheline nurk
- Ülesanne 213
- Paralleelsed tasandid
- Kahe tasandi vaheline nurk
- Kahetahuline nurk
- Kolmnurga projektsioon tasandil I
- Kolmnurga projektsioon tasandil II
Hulktahukad ja pöördkehad