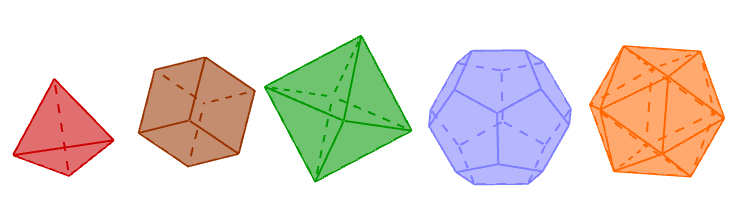
Regelmatige veelvlakken
Een ruimtefiguur die volledig begrensd wordt door platte grensvlakken noemt men een veelvlak.
Een kubus en een piramide zijn voorbeelden van veelvlakken, maar een cilinder is geen veelvlak.
Aan de regelmatige veelvlakken, ook Platonische veelvlakken genoemd, worden een aantal strengere voorwaarden opgelegd:
1. Alle zijvlakken zijn regelmatige veelhoeken.
2. Alle zijvlakken zijn congruent.
3. Alle hoekpunten zijn congruent (in elke hoek van het veelvlak komen evenveel zijvlakken samen).
4. Het veelvlak is convex.
In 550 v. Chr. waren de kubus (zesvlak), de tetraëder (viervlak) en de dodecaëder (twaalfvlak) al gekend door Pythagoras. Anderhalve eeuw later heeft de Griekse filosoof Plato hieraan de icosaëder (twintigvlak) en de octaëder (achtvlak) toegevoegd.