Producto Cruz (Vectorial) y sus aplicaciones

Definición

Se llama producto vectorial o producto cruz de vectores v y w el vector

. Cuya longitud equivale al área del paralelogramo constuído en vectores v y w. Y el vector resultante es perpendicular al plano de estos vectores.

Para obtener el producto vectorial entre u y v:

Se colocan las componentes de ambos vectores como elementos de una matriz.
Las componentes del vector resultante: obtén una submatriz que contenga todas las componentes de la matriz original excepto la columna con la componente a calcular, es decir: Sí deseo la componente en x, mi submatriz contendrá las columnas de y y z. Sí deseo la componente en y, mi submatriz contendrá las columnas de x y z. Sí deseo la componente en z, mi submatriz contendrá las columnas de x y y.
Calcular la determinante de cada submatriz obtenida en el paso anterior.
El resultado será un vector en R³.

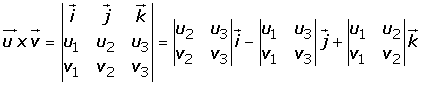
El módulo del producto vectorial de dos vectores v y w equivale al área del paralelogramo construído en estos vectores.
El producto vectorial de dos vectores que no son nulos v y w equivale a cero sólo cuando los vectores son colineales (igual dirección).
El producto vectorial de los vectores v y w es perpendicular a estos vectores. es y