Ecuaciones exponenciales
Resolución de dos ecuaciones exponenciales: una sin aplicar logaritmos y otro aplicando logaritmos.
Ecuación 1
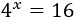
Escribimos 16 como la potencia 2^4 y la base de la exponencial 4^x como 2^2 para tener bases comunes:
Escribimos 16 como la potencia 2^4 y la base de la exponencial 4^x como 2^2 para tener bases comunes:
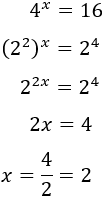
En los últimos pasos hemos igualado los exponentes porque tenemos dos potencias con la misma base. Por tanto, son iguales cuando sus exponentes son iguales.
En los últimos pasos hemos igualado los exponentes porque tenemos dos potencias con la misma base. Por tanto, son iguales cuando sus exponentes son iguales. Ecuación 2
En esta ecuación no se pueden igualar los exponentes porque las bases son distintas (3 y 5).
Aplicamos logaritmos en la ecuación para ayudarnos de sus propiedades.
Si dos números son iguales, entonces, sus logaritmos son iguales:
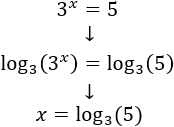
En este caso hemos aplicado logaritmo de base 3 para que el logaritmo del lado izquierdo se cancela. Pero se pueden aplicar logaritmos con base distinta, por ejemplo, con base 10.
En este caso hemos aplicado logaritmo de base 3 para que el logaritmo del lado izquierdo se cancela. Pero se pueden aplicar logaritmos con base distinta, por ejemplo, con base 10.
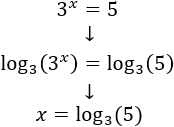
En este caso hemos aplicado logaritmo de base 3 para que el logaritmo del lado izquierdo se cancela. Pero se pueden aplicar logaritmos con base distinta, por ejemplo, con base 10.
En este caso hemos aplicado logaritmo de base 3 para que el logaritmo del lado izquierdo se cancela. Pero se pueden aplicar logaritmos con base distinta, por ejemplo, con base 10. Enlaces
- Ecuaciones exponenciales resueltas
- Teorema de Pitágoras (con problemas resueltos)
- Fracciones equivalentes y fracción irreductible
- Potencias (propiedades y ejercicios)
- Ecuaciones de primer grado explicadas
- Problemas resueltos de ecuaciones
- Sistemas de ecuaciones (métodos)
- Problemas resueltos de sistemas de ecuaciones
- Ecuaciones de segundo grado resueltas
- Ecuaciones bicuadradas resueltas
- Problemas de progresiones o sucesiones
- Problemas resueltos de mcm y mcd
- Problemas resueltos de trigonometría (seno, coseno y tangente)
- Problemas de movimiento rectilíneo uniforme (MRU)
- Integrales resueltas (directas, por sustitución y por partes)
- Números complejos o imaginarios