CIRCONFERENZA
Definizone: luogo geometrico dei punti del piano equidistanti da un punto detto centro.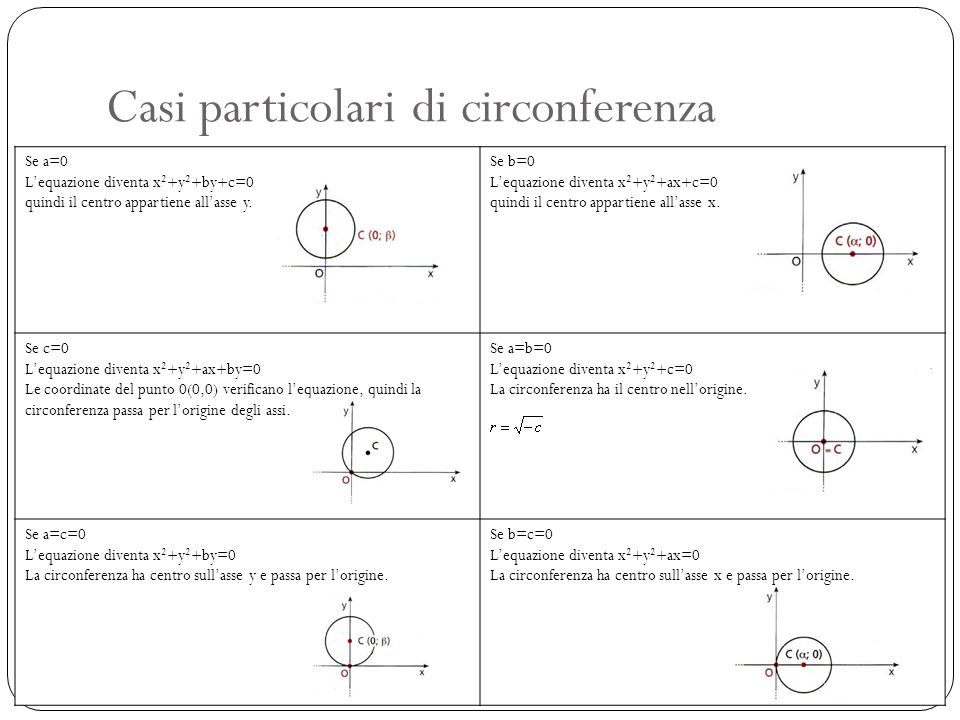 -Rette e circonferenze(posizioe di una retta).
La posizone di una retta dipende dalla distanza "d" del centro della circonferenza della rettta, cioè dalla misura del segmento che ha per estremi il centro e il piede della perpendicolare condotta dal centro alla retta.
-Rette e circonferenze(posizioe di una retta).
La posizone di una retta dipende dalla distanza "d" del centro della circonferenza della rettta, cioè dalla misura del segmento che ha per estremi il centro e il piede della perpendicolare condotta dal centro alla retta.


 -Quarto metodo ; formule di sdoppiamento.
-Quarto metodo ; formule di sdoppiamento.
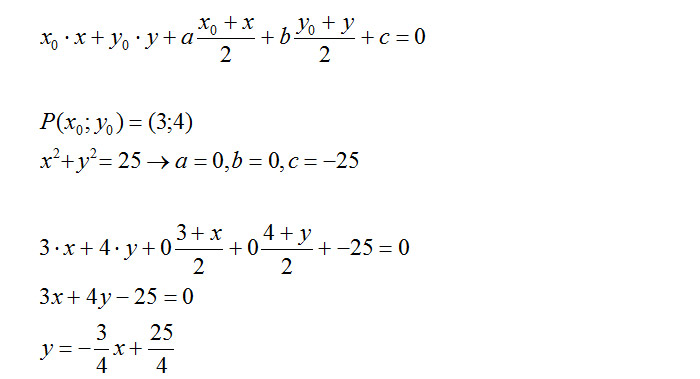 -Determinare l'equazione di una circonferenza
-Determinare l'equazione di una circonferenza

Equazione generale: x2+y2+ax+bx+c=0
r= solo se Se allora, r=0 e la circonferenza si riduce a un solo punto,quindi la circonferenza è degenere. -Casi particolari. -Rette e circonferenze(posizioe di una retta).
La posizone di una retta dipende dalla distanza "d" del centro della circonferenza della rettta, cioè dalla misura del segmento che ha per estremi il centro e il piede della perpendicolare condotta dal centro alla retta.
-Rette e circonferenze(posizioe di una retta).
La posizone di una retta dipende dalla distanza "d" del centro della circonferenza della rettta, cioè dalla misura del segmento che ha per estremi il centro e il piede della perpendicolare condotta dal centro alla retta.



 -Quarto metodo ; formule di sdoppiamento.
-Quarto metodo ; formule di sdoppiamento.
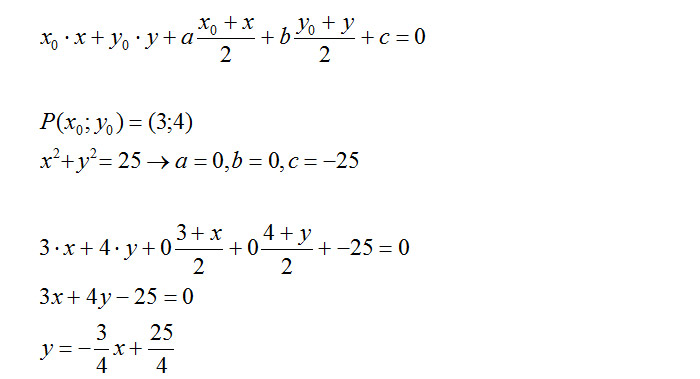 -Determinare l'equazione di una circonferenza
-Determinare l'equazione di una circonferenza

-Posizione di due circonferenze

 -Fasci di circonferenze.
-Fasci di circonferenze.
 L'insieme costituito da queste infinite circonferenze viene detto fascio di circonferenze con generatrici e '.
L'insieme costituito da queste infinite circonferenze viene detto fascio di circonferenze con generatrici e '.
x+++4ky+%E2%80%93+16+%E2%80%93+34k+=+0+..jpg) -Studio di un fascio di circonferenze.
Per studiare un fascio di circonferenze occore:
a)centro e raggio in funzione di k
b) le due generatrici
c)gli eventuali punti base
d)l'asse radicale e l'asse centrale
e)eventuali circonferenze degeneri
Una circonferenza degenere può essere una retta (ciconferenza di raggio infinitamente grande) oppure un punto (circonferenza di raggio nullo).
-Studio di un fascio di circonferenze.
Per studiare un fascio di circonferenze occore:
a)centro e raggio in funzione di k
b) le due generatrici
c)gli eventuali punti base
d)l'asse radicale e l'asse centrale
e)eventuali circonferenze degeneri
Una circonferenza degenere può essere una retta (ciconferenza di raggio infinitamente grande) oppure un punto (circonferenza di raggio nullo).

 -Fasci di circonferenze.
-Fasci di circonferenze.
 L'insieme costituito da queste infinite circonferenze viene detto fascio di circonferenze con generatrici e '.
L'insieme costituito da queste infinite circonferenze viene detto fascio di circonferenze con generatrici e '.
x+++4ky+%E2%80%93+16+%E2%80%93+34k+=+0+..jpg) -Studio di un fascio di circonferenze.
Per studiare un fascio di circonferenze occore:
a)centro e raggio in funzione di k
b) le due generatrici
c)gli eventuali punti base
d)l'asse radicale e l'asse centrale
e)eventuali circonferenze degeneri
Una circonferenza degenere può essere una retta (ciconferenza di raggio infinitamente grande) oppure un punto (circonferenza di raggio nullo).
-Studio di un fascio di circonferenze.
Per studiare un fascio di circonferenze occore:
a)centro e raggio in funzione di k
b) le due generatrici
c)gli eventuali punti base
d)l'asse radicale e l'asse centrale
e)eventuali circonferenze degeneri
Una circonferenza degenere può essere una retta (ciconferenza di raggio infinitamente grande) oppure un punto (circonferenza di raggio nullo).